Fourier.exe
la dualità tra tempo e frequenza

"Fondamentalmente, la dualità consiste nel fornire due punti di vista per descrivere lo stesso oggetto."
Questo programma esegue e visualizza la trasformata e l'antitrasformata discreta di Fourier.
Il segnale di partenza $F(t)$ con $t \in \mathbb{N}$ viene disegnato a mano nel riquadro in alto a sinistra, in rosso. Se il riquadro è largo $T$ pixel, avremo $T$ campionamenti nel tempo del segnale e $t$ prenderà i valori da $0$ a $T - 1$.

La trasformata
La trasformata $\widehat F(f)$ con $f$ che prende i valori da $-T / 2$ a $T / 2 - 1$, è un numero complesso che ha quindi due componenti, una parte reale e una parte immaginaria (se la rappresentazione geometrica dei numeri complessi non ti è familiare potrebbe interessarti il mio programma Argand.exe). Tali componenti possono essere calcolate separatamente utilizzando le funzioni trigonometriche. In particolare per ogni valore di $f$ si ha rispettivamente $$ \begin{alignedat}{2} \text{Re} \! \left( \widehat F(f) \right) = &\sum_t F(t) \cos \left( \omega \, t \right) \\ \text{Im} \! \left( \widehat F(f) \right) = &\sum_t F(t) \sin \left( \omega \, t \right) \end{alignedat} $$ dove $\omega = 2 \, \pi \, f / T$ è detta pulsazione e $t$ va da $0$ a $T - 1$. Queste due componenti sono sfasate di $\pi / 2$, sono quindi ortogonali e permettono di "cogliere" le componenti ad una determinata frequenza indipendentemente dalla fase. Infatti utilizzando la nota identità $\cos \left( a + b \right) = \cos a \cos b - \sin a \sin b$ si vede che $$ A \cos \left( \omega \, t + \theta \right) = X \cos \left( \omega \, t \right) + Y \sin \left( \omega \, t \right) $$ dove $X = A \cos \theta$ e $Y = -A \sin \theta$. Quindi una sinusoide a una data frequenza con fase arbitraria può sempre essere rappresentata da un'opportuna combinazione lineare di due sinusoidi della medesima frequenza sfasate di $\pi / 2$ (seno e coseno, appunto).
Grazie alla famosa formula di Eulero $$ e^{i \, \theta} = \cos \theta + i \sin \theta $$ è possibile scrivere sinteticamente $$ \widehat F(f) = \sum_t F(t) e^{-i \, \omega \, t} $$
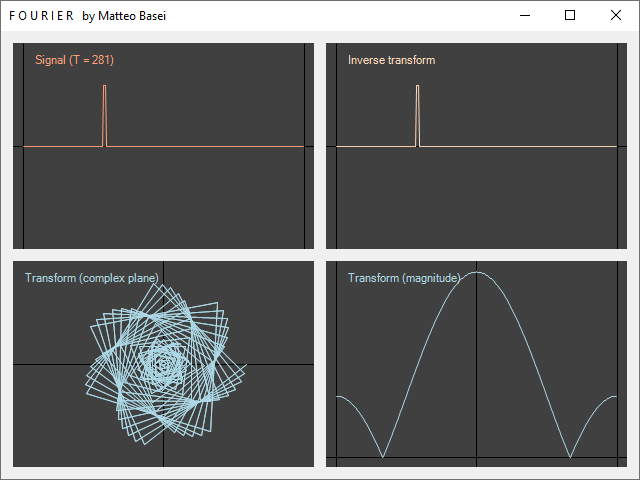
Nei due riquadri in basso, in azzurro, viene mostrata la trasformata, che essendo una funzione complessa a varibile reale (la frequenza), ha un grafico tridimensionale (un asse per la variabile e due assi per l'immagine).
Nel riquadro a sinistra viene rappresentato il piano complesso con l'asse della frequenza perpendicolare ad esso. Con questo tipo di visualizzazione si può ottenere un interessante rappresentazione di come funziona la trasformata di Fourier (vedi F-Paint).
Nel riquadro di destra si ha invece la frequenza in ascissa e il modulo in ordinata, cioè il classico grafico in frequenza che siamo abituati a vedere (ad esempio in ambito musicale, negli equalizzatori grafici).
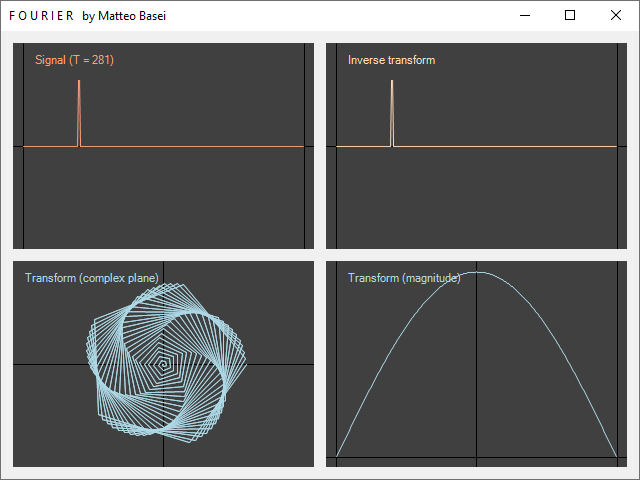
L'antitrasformata
Per riottenere il segnale di partenza $F(t)$ in funzione del tempo $t$ si esegue la somma dei termini della trasformata moltiplicati per $e^{i \, \omega \, t}$, dividendo poi il risultato per $T$ $$ F(t) = \frac{1}{T} \sum_f \widehat F(f) e^{i \, \omega \, t} $$ con $f$ che prende ancora i valori da $-T / 2$ a $T / 2 - 1$.
Si noti come, a meno del fattore costante (che si può comunque rendere simmetrico utilizzando $1 / \sqrt{T}$ in entrambe le formule) e il segno del'esponente di $e$, la formula dell'antitrasformata sia identica a quella della trasformata. Le rappresentazioni nel tempo e in frequenza di un segnale sono perfettamente intercambiabili. Questo è solo uno dei molti esempi in cui in matematica si presenta il concetto di dualità.
Nel riquadro in alto a destra è mostrata in arancione l'antitrasformata, per poterla confrontare con il segnale originale.
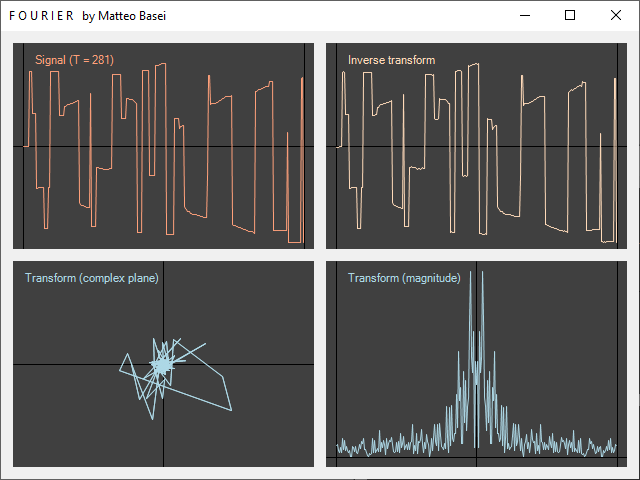
La simmetria della trasformata
Nel grafico del modulo della trasformata in basso a destra si può notare come le frequenze negative (prima metà del grafico) siano simmetriche rispetto a quelle positive (seconda metà). Il motivo di ciò sta nel fatto che il segnale di partenza è reale. Le componenti a frequenza positiva $f$, che al variare di $t$ completano una rotazione in senso antiorario $f$ volte al secondo, sono il complesso coniugato delle corrispondenti componenti a frequenza negativa $-f$, che ruotano in senso orario alla stessa velocità. Quindi $$ \widehat F(f) = \widehat F(-f)^* $$ e visto che la somma tra un numero complesso e il rispettivo complesso coniugato da sempre risultato reale, questo è coerente con il fatto che sommando tutte le componenti (eseguendo cioè l'antitrasformata) il risultato sia sempre reale come il segnale di partenza. Inoltre essendo uguali i moduli di un numero complesso e del rispettivo complesso coniugato si ha $$ \left| \widehat F(f) \right| = \left| \widehat F(-f) \right| $$ che corrisponde alla simmetria del grafico.
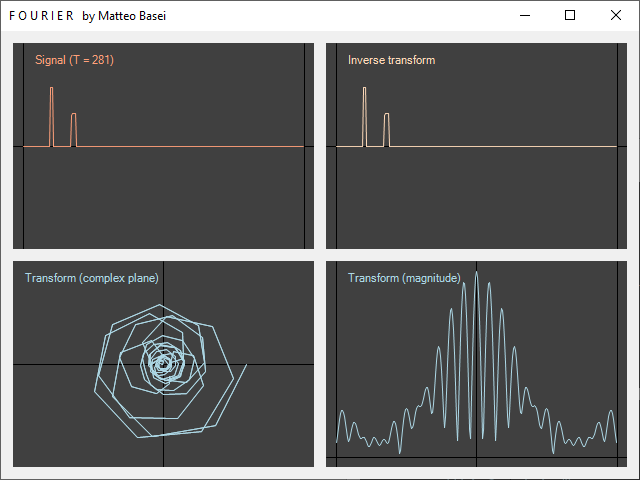
Inoltre il fatto che partendo da $T$ campionamenti di un segnale reale siano sufficienti solo $T / 2$ valori complessi, ognuno dei quali costituito da $2$ componenti, era già prevedibile per mantenere il numero di "gradi di libertà" del segnale.