Lagrange i punti di equilibrio lagrangiani nel problema dei tre corpi ristretto
Il cosiddetto problema dei due corpi, vale a dire lo studio, in meccanica classica, di un sistema costituito da due corpi di massa $m_1$ e $m_2$ che interagiscono secondo la legge di gravitazione universale di Newton, è facilmente risolvibile analiticamente, essendo equivalente al moto di un corpo di massa $\frac{m_1 \, m_2}{m_1 + m_2}$ (detta massa ridotta) e di coordinate $r_2 - r_1$ in un campo centrale dato. Integrando si ottiene l'equazione di una sezione conica e quindi le leggi già dedotte empiricamente da Keplero all'inizio del XVII secolo (vedi Tsiolkovsky.exe per ulteriori considerazioni sulla meccanica orbitale).
Se si aggiunge un terzo corpo si ottiene un sistema che in generale non è più risolvibile, nel senso che le soluzioni analitiche, pur esistendo, non possono più essere rappresentate con un numero finito di termini. In generale il problema può essere affrontato con tecniche perturbative (in sostanza si suddivide il problema in due parti, una risolvibile analiticamente, l'altra esprimibile sotto forma di una serie di potenze) o con il calcolo numerico (vedi ad esempio Newton.exe). Il sistema può presentare, in base alle condizioni iniziali, dei comportamenti caotici (vedi Fractals).
Il problema dei tre corpi ristretto
Si parla di problema dei tre corpi ristretto quando si considera trascurabile la massa del terzo corpo. In questo caso possiamo risolvere il problema dei due corpi $m_1$ e $m_2$ e considerare il moto del terzo corpo nel campo dato da tale soluzione. L'hamiltoniana per un corpo di massa $m$ in tale campo è data da $$ \mathcal{H} = \frac{1}{2 \, m} p^2 - \frac{G \, m \, m_1}{r_1} - \frac{G \, m \, m_2}{r_2} $$ dove $p$ è la quantità di moto del corpo e $r_1$ e $r_2$ indicano le distanze da $m_1$ e $m_2$ rispettivamente.
Per semplicità consideriamo il caso in cui $m_1$ e $m_2$ siano in orbita circolare (ma i punti di equilibrio lagrangiano sussistono anche nel caso di orbita ellittica) e il terzo corpo si trovi inizialmente nel piano in cui giace l'orbita con velocità iniziale giacente nel piano stesso. In questo caso le equazioni mostrano che il moto resterà sempre nel piano orbitale, com'è naturale aspettarsi. Scegliamo quindi un sistema di riferimento non inerziale solidale con il moto di $m_1$ e $m_2$, quindi in moto rotatorio uniforme attorno al baricentro del sistema. Se $\omega$ è lo pseudovettore velocità angolare in tale sistema di riferimento l'energia diventa $$ \mathcal{H} = \frac{1}{2\, m} p^2 + p \cdot \left( \omega \times r \right) - \frac{G \, m \, m_1}{r_1} - \frac{G \, m \, m_2}{r_2} $$ Il prodotto vettoriale tra la velocità angolare e le coordinate è $$ \omega \times r = \left( \begin{array}{c} \omega_y \, z - \omega_z \, y \\ \omega_z \, x - \omega_x \, z \\ \omega_x \, y - \omega_y \, x \end{array} \right) $$ che per la scelta del nostro sistema di riferimento, in cui solo la componente $z$ di $\omega$ è diversa da zero, si riduce a $$ \omega \times r = \left( \begin{array}{c} -\omega_z \, y \\ \omega_z \, x \\ 0 \end{array} \right) $$ e allo stesso modo si riduce l'espressione dell'energia cinetica per la scelta di considerare solo traiettorie del terzo corpo nel piano orbitale, cioè traiettorie in cui $p_z = 0$, quindi $$ \mathcal{H} = \frac{1}{2 \, m} \left( {p_x}^2 + {p_y}^2 \right) - p_x \, \omega_z \, y + p_y \, \omega_z \, x - \frac{G \, m \, m_1}{r_1} - \frac{G \, m \, m_2}{r_2} $$
Scegliamo ora l'unità di massa pari alla somma delle due masse e indichiamo con $\mu$ la massa del corpo più piccolo. In questo modo $m_2 = \mu$ e $m_1 = 1 - \mu$. Scegliamo inoltre l'unità di lunghezza pari alla distanza tra le due masse. Scegliamo infine l'orientamento del sistema di riferimento in modo tale che $m_1$ risulti nel semiasse positivo dell'asse $x$, e di conseguenza $m_2$ sarà nel semiasse negativo. In questo modo $m_1$ sarà in $\left( \mu , 0 \right)$, mentre $m_2$ sarà in $\left( -1 + \mu , 0 \right)$. Infine, per semplificare ulteriormente le formule, scegliemo unità di misura tali per cui $G = 1$. Avendo già fissato l'unità di lunghezza e di massa ciò equivale a fissare l'unità di tempo. Con questa scelta, ricordando la terza legge di Keplero sulla relazione tra semiasse maggiore $a$ e periodo $T$ $$ \frac{T^2}{a^3} = \frac{4 \, \pi^2}{G \left( m_1 + m_2 \right)} $$ si ottiene un'orbita con periodo $T = 2 \, \pi$ e di conseguenza anche $\omega_z = 1$. Otteniamo quindi: $$ \mathcal{H} = \frac{1}{2} \left( {p_x}^2 + {p_y}^2 \right) - p_x \, y + p_y \, x - \frac{1 - \mu}{\sqrt{ \left( x - \mu \right)^2 + y^2 }} - \frac{\mu}{\sqrt{ \left( x + 1 - \mu \right)^2 + y^2 }} $$ A questo punto le equazioni canoniche per $\dot x$ e $\dot y$ ci danno $$ \dot x = \frac{\partial \mathcal{H}}{\partial p_x} = p_x - y , \quad \dot y = \frac{\partial \mathcal{H}}{\partial p_y} = p_y + x $$ che sostituite nei primi due termini $$ \begin{array}{l} \frac{1}{2} \left( \left( \dot x + y \right)^2 + \left( \dot y - x \right)^2 \right) - \left( \dot x + y \right) y + \left( \dot y - x \right) x = \\ = \frac{1}{2} \left( {\dot x}^2 + 2 \, \dot x \, y + y^2 + {\dot y}^2 - 2 \, \dot y \, x + x^2 - 2 \, \dot x \, y - 2 \, y^2 + 2 \, \dot y \, x - 2 \, x^2 \right) = \\ = \frac{1}{2} \left( {\dot x}^2 + {\dot y}^2 - x^2 - y^2 \right) \end{array} $$ ci permettono di ottenere infine l'espressione $$ \mathcal{H} = \frac{{\dot x}^2 + {\dot y}^2}{2} - \frac{x^2 + y^2}{2} - \frac{1 - \mu}{\sqrt{ \left( x - \mu \right)^2 + y^2 }} - \frac{\mu}{\sqrt{ \left( x + 1 - \mu \right)^2 + y^2 }} $$
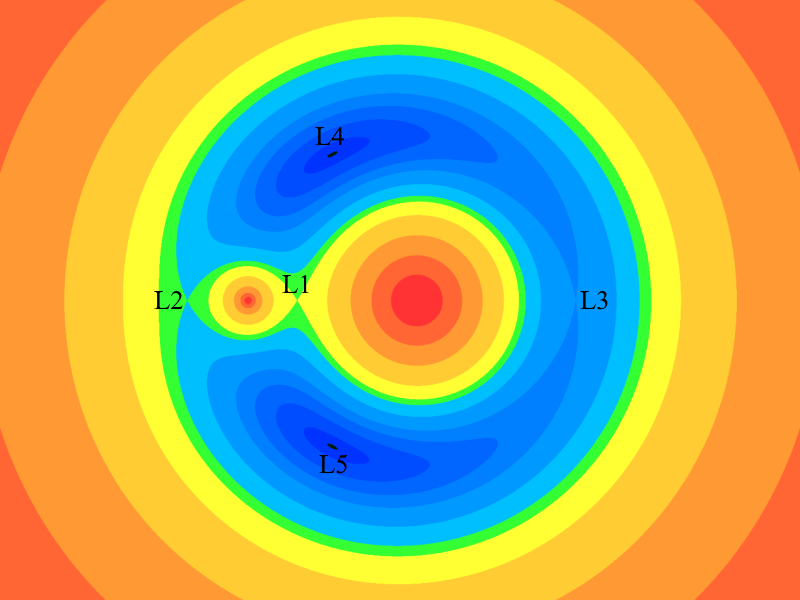
Otteniamo quindi la seguente funzione di $x$ e di $y$ dipendente dal parametro $\mu$ che rappresenta il potenziale efficace nel sistema di riferimento rotante $$ \varphi \left( x , y \right) = -\frac{x^2 + y^2}{2} - \frac{1 - \mu}{\sqrt{ \left( x - \mu \right)^2 + y^2 }} - \frac{\mu}{\sqrt{ \left( x + 1 - \mu \right)^2 + y^2 }} $$
Il primo termine, in cui compaiono solo le coordinate, corrisponde all'energia centrifuga dovuta al moto rotatorio del sistema di riferimento. I successivi due termini, in cui compaiono le masse $m_1 = 1 - \mu$ e $m_2 = \mu$, corrispondono invece all'energia potenziale dovuta alle due masse collocate sull'asse $x$ in $\left( \mu , 0 \right)$ e $\left( -1 + \mu , 0 \right)$.
Per visualizzare questa funzione ho scritto uno shader in GLSL utilizzando dei colori per evidenziare i punti stazionari. Ho poi riutilizzato (impropriamente) ImMap per averne una versione 3D.


I punti di equilibrio lagrangiani
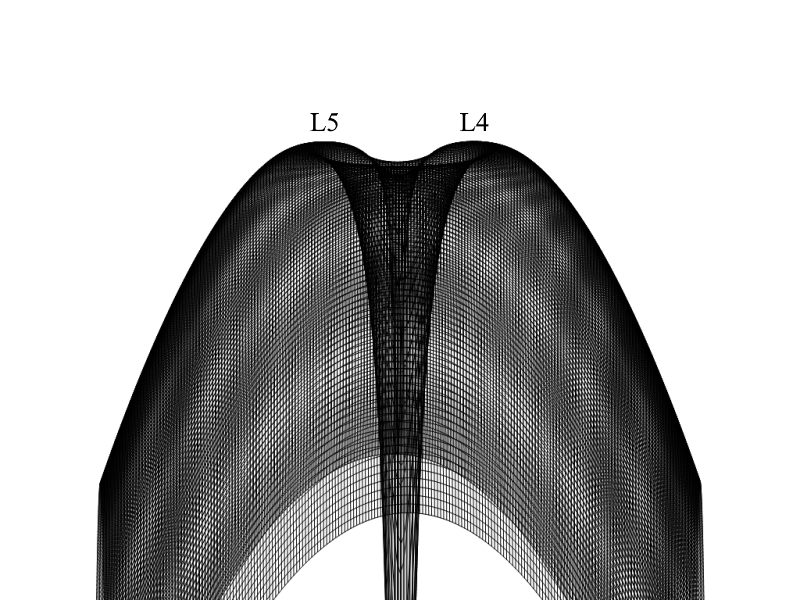
La funzione ottenuta ha due massimi e tre punti di sella. I tre punti di sella corrisponderanno a tre punti di equilibrio instabile. Essi sono collineari a $m_1$ e $m_2$ e sono chiamati L1, L2 e L3. L1 è posto tra $m_1$ e $m_2$, L2 è all'esterno dell'orbita di $m_2$, mentre L3 è opposto a $m_2$ rispetto a $m_1$.
I due massimi corrisponderanno ad altri due punti di equilibrio. Sono disposti in modo da formare due triangoli equilateri con $m_1$ e $m_2$ e per questo sono chiamati anche punti lagrangiani triangolari. Sono indicati con L4 e L5 e precedono e seguono di 60° $m_2$ nella sua orbita.
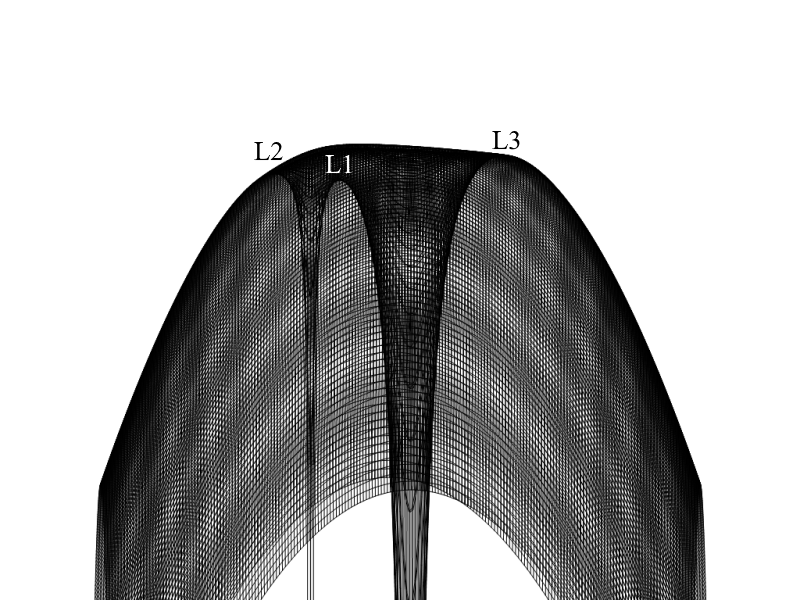
Pur essendo punti di equilibrio instabili tali punti permettono l'esistenza di traiettorie in oscillazione intorno ad essi, dette orbite di Lissajous in quanto la traiettoria risultante corrisponde alle figure omonime (vedi Lissajous.exe).
Nel sistema solare osserviamo molti asteroidi e satelliti nei punti lagrangiani di differenti sistemi. Il caso più eclatante è quello della grande moltitudine di asteroidi in orbita nei dintorni dei punti L4 e L5 del sistema Sole - Giove, chiamati asteroidi troiani. Altri esempi si possono ritrovare nei satelliti di Saturno: due piccolissime lune, Telesto e Calipso, condividono l'orbita di Teti nei punti L4 e L5. Infine recentemente è stato scoperto che anche la Terra ha due asteroidi troiani in L4, chiamati 2010 TK7 e 2020 XL5.