R-Paint gli algoritmi ricorsivi

"L'iterazione è umana, la ricorsione è divina."

Gli algoritmi ricorsivi sono probabilmente una delle prime cose che un programmatore si ritrova ad imparare. Utilizzarli per realizzare semplici programmi che generano curve frattali (vedi Fractals per altri frattali da me realizzati) permette tra l'altro di "toccarne con mano" una chiara interpretazione geometrica.

Se da una parte sono algoritmi semplici da realizzare, dall'altra possono dare lo spunto per approfondire importanti idee matematiche. Sono infatti ricollegabili, oltre alla teoria dei linguaggi formali, anche a concetti tutt'altro che banali riguardanti i fondamenti, la topologia e la nozione di misura, come si evince dagli importanti nomi associati ad alcuni di questi frattali, come Cantor, Hilbert e Peano.

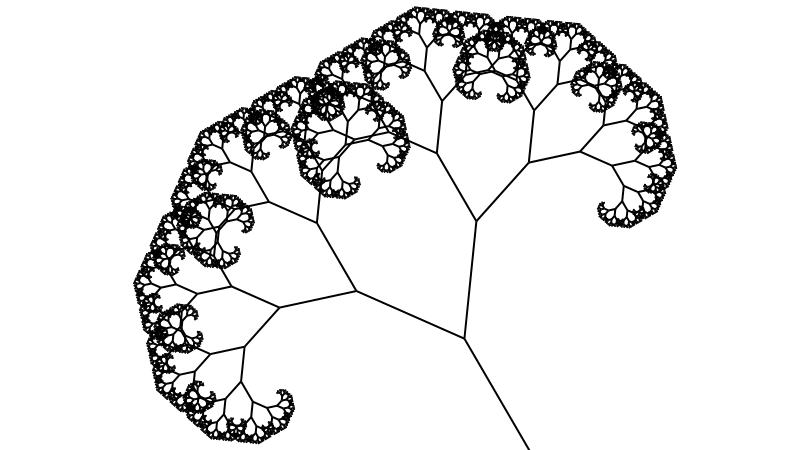
Sistemi di Lindenmayer

[...]

Un sistema di Lindenmayer (o L-system) è definito come l'ennupla ordinata $\left( A , \alpha , r \right)$ dove:

• $A$ è un insieme di simboli chiamato alfabeto;
• $\alpha \in A$ è il simbolo iniziale, chiamato anche assioma;
• $r$ è la regola di riscrittura, cioè una relazione $r \subseteq A^* \times A^*$, dove ${}^*$ è l'operatore di Kleene, cioè un operatore tale che $A^*$ sia l'insieme di tutte le stringhe finite costruibili utilizzando l'alfabeto $A$.

I simboli che compaiono a sinistra nella relazione $r$ sono chiamati variabili, quelli che non vi compaiono sono invece chiamati costanti.

[...]

Dimensione algebrica, topologica e frattale

Il concetto intuitivo di dimensione (un segmento è uno spazio $1$-dimensionale, un quadrato è $2$-dimensionale, un cubo $3$-dimensionale, eccetera) può essere formalizzato in modi differenti. La dimensione di uno spazio vettoriale è la cardinalità di una sua base, vale a dire il numero di coordinate necessarie a specificarne un elemento. Questa nozione, che viene a volte chiamata dimensione algebrica, si estende naturalmente ad uno spazio affine (che "eredita" la dimensione dello spazio vettoriale con cui è definito) e di conseguenza ad una varietà connessa (la dimensione della varietà è la dimensione dello spazio affine a cui è localmente omeomorfa o, per le varietà differenziabili, la dimensione dello spazio tangente in ogni punto).

È possibile dare delle definizioni più generali di dimensione, applicabili a spazi topologici, in modo che la dimensione diventi appunto una proprietà topologica (quindi invariante per omeomorfismi, gli isomorfismi tra spazi topologici). Si parlerà in questo caso di dimensione topologica. Una di queste possibili definizioni è data dalla dimensione di Lebesgue. La dimensione di Lebesgue di uno spazio topologico $X$ è il più piccolo intero $n$ tale che ogni ricoprimento aperto di $X$ ha un raffinamento $\left\{ U_i \right\}$ in cui ogni punto $x \in X$ è contenuto in al più $n + 1$ elementi di $\left\{ U_i \right\}$. Un'altra possibile definizione, dovuta a Brouwer, è data in modo ricorsivo. Si assegna dimensione $-1$ all'insieme vuoto e si definisce poi la dimensione di uno spazio $X$ come il più piccolo intero $n$ tale che ogni punto $x \in X$ abbia un intorno arbitrariamente piccolo la cui frontiera ha dimensione minore o uguale a $n - 1$.

Esistono delle ulteriori definizioni di dimensione legate questa volta alla nozione di misura. Per comprenderle partiamo da una considerazione particolarmente banale: se ingrandiamo di un fattore $2$ un segmento la sua lunghezza raddoppia. Se lo ingrandiamo di un fattore $3$ triplica. In generale se lo ingrandiamo di un fattore $k$ la sua lunghezza aumenta di un fattore $k$. Se ingrandiamo di un fattore $k$ un quadrato la sua area aumenta invece di un fattore $k^2$. Ingrandendo un cubo di un fattore $k$ il suo volume aumenta di un fattore $k^3$. Tutto ciò vale anche per spazi dalle forme meno regolari (ma, come vedremo, "abbastanza" regolari), quali curve, superfici, solidi, eccetera.

In generale ingrandendo di un fattore $k$ uno spazio $n$-dimensionale la sua misura $n$-dimensionale aumenta di un fattore $k^n$. Si potrebbe quindi definire la dimensione come quel numero $n$ tale per cui ingrandendo di un fattore $k$ uno spazio la sua misura cresce di un fattore $k^n$. Esiste più di una defizione formale, quali la dimensione di Hausdorff o la dimensione di Minkowski-Bouligand, che possono essere indicate genericamente come dimensione frattale.

La curva di Koch

La curva di Koch è tra i frattali più semplici. A differenza degli alberi ricorsivi visti in precedenza viene costruita tramite operazioni di sostituzione. Si parte da un segmento e lo si sostituisce con $4$ segmenti in questo modo: si divide in $3$ il segmento di partenza e si sostituisce la parte centrale con due segmenti di ugual misura posizionati come i lati del triangolo equilatero la cui base è il segmento centrale rimosso. Si procede poi ricorsivamente sui $4$ segmenti ottenuti.

Se ingrandiamo di un fattore $3$ la curva di Koch ci ritroviamo con $4$ copie identiche della figura di partenza. Abbiamo quindi una curva che, pur continuando ad avere dimensione topologica $1$, in un certo senso si "comporta" come se avesse dimensione $n$ tale che $3^n = 4$, quindi $n = \log_3{4}$ che è approssimativamente uguale a $1.26$.

In questo caso quindi le differenti definizioni di dimensione, che davano i medesimi risultati per gli spazi "regolari", non coincidono. Un frattale è definito come uno spazio la cui dimensione frattale è strettamente maggiore della propria dimensione topologica.

La caratteristica fondamentale che rende questo possibile è il fatto che la curva di Koch è ottenuta attraverso un procedimento infinito, in questo caso in particolare da un algoritmo ricorsivo. Solo ripetendo infinite volte il procedimento i $4$ pezzi sono identici alla figura iniziale, in caso contrario possono esserlo solo approssimativamente e la lunghezza dell'approssimativa curva di Koch torna ad essere $3$ volte quella della figura originale.

Il triangolo e il tappeto di Sierpinski

[...]

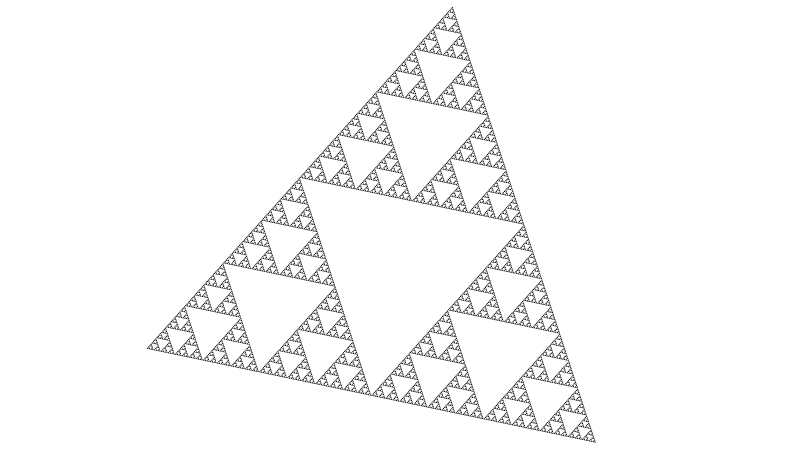
Triangolo di Sierpinski $\log_2 3$ circa $1.58$.

[...]

Tappeto di Sierpinski $\log_3 8$ circa $1.89$ (versione tridimensionale: spugna di Menger).

[...]

La sequenza scelta in questa pagina (curva di Koch, triangolo di Sierpinski, tappeto di Sierpinski) non è casuale. Le rispettive dimensioni frattali sono approssimativamente $1.26$, $1.58$ e $1.89$ e si può notare come queste figure siano via via più "dense" mano a mano che la dimensione si avvicina a $2$. Viene naturale chiedersi se esisono curve con dimensione frattale $2$.

Curve che riempiono il piano

Curva del drago di Heighway. Curva di Peano (varie versioni, curva di Hilbert).

[...]

[...]

[...]