Tsiolkovsky.exe simulatore di lanci spaziali

"La Terra è la culla dell'umanità, ma chi può vivere per sempre in una culla?"

Un buon modo per scegliere il nome di un progetto è omaggiare un grande protagonista della storia, un pioniere o una figura fondamentale nell'ambito in cui si colloca il progetto. Per un simulatore di lanci spaziali la scelta non può che ricadere nel grande scienziato russo Konstantin Tsiolkovsky, pioniere dell'astronautica, tra i più importanti insieme a Goddard, Oberth e von Braun. La sua opera più famosa è "L'esplorazione dello spazio per mezzo di motori a reazione" del 1903, dove applica per la prima volta l'equazione che ora porta il suo nome al moto di un razzo spaziale.

L'obiettivo di questo programma è simulare, nei suoi punti essenziali, il lancio di un razzo spaziale. In particolare simulare i lanci più importanti nella storia dell'astronautica, confrontando poi i dati della simulazione con i dati reali.

In questa pagina mi concentrerò nella descrizione degli aspetti della simulazione legati al volo spaziale. Se ti interessa il modo in cui vengono simulate le leggi della dinamica e della gravità in generale, cosa che naturalmente sta alla base di questo programma, puoi invece dare un'occhiata alla pagina di un mio altro progetto: Newton.exe, che condivide con Tsiolkovsky.exe il relativo codice (e pure la strategia di scelta del nome).

Meccanica orbitale

Mandare in orbita del carico utile, come una navicella o un satellite, consiste in sostanza nel portarlo ad una determinata quota superiore alla linea di Karman (100 km, considerato il limite superiore dell'atmosfera terrestre) raggiungendo una certa velocità, dipendente dalla quota stessa, tale per cui il carico non ricada sulla Terra. Le altissime velocità richieste per restare in orbita, nell'ordine delle decine di migliaia di km all'ora, rappresentano la vera sfida da superare, più che la quota in sé.

Dai 200 ai 2000 km si parla di orbita bassa (LEO, Low Earth Orbit). Ad esempio la Stazione Spaziale Internazionale (ISS, International Space Station) orbita ad una quota media di poco superiore a 400 km, che corrisponde ad una velocità di circa 27600 km/h. Al di sopra, dai 2000 fino ai 35000 km si parla di orbita media (MEO, Medium Earth Orbit). Ad esempio i satelliti GPS orbitano a circa 20000 km di quota.

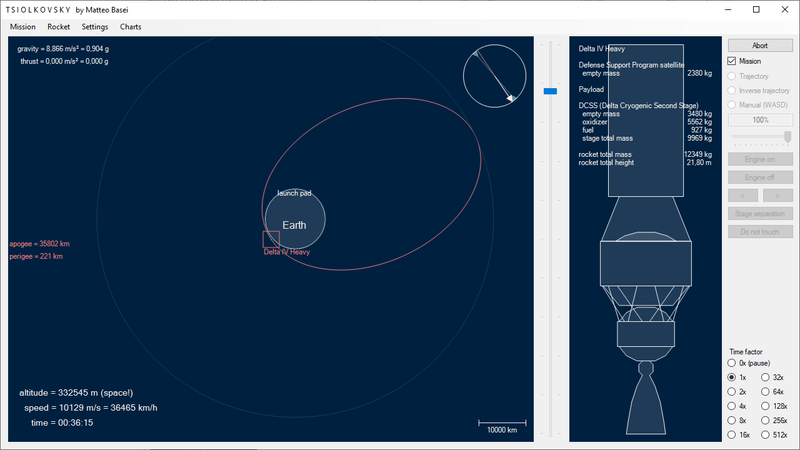
A 35786 km si trova l'orbita geostazionaria (GEO, Geosynchronous Equatorial Orbit). Essa è un'orbita circolare ed equatoriale con un periodo di esattamente un giorno siderale (il tempo in cui la Terra compie una rotazione completa su sé stessa, leggermente inferiore al giorno solare a causa del moto della Terra intorno al Sole). Di conseguenza un oggetto in tale orbita resta sempre al di sopra del medesimo punto della Terra. La velocità orbitale corrispondente è di circa 11000 km/h. L'utilizzo dell'orbita geostazionaria è stato ipotizzato dal grande scrittore di fantascienza Arthur C. Clarke, autore di 2001: odissea nello spazio e dei romanzi del ciclo di Rama.

L'orbita circolare è solo un caso particolare, seppur notevole, di possibile traiettoria di due corpi sottoposti alla forza di gravitazione. Il cosiddetto problema dei due corpi, due corpi sottoposti a forze dipendenti solo dalla distanza tra di essi, con un semplice cambio di variabili può essere ricondotto al problema di un singolo corpo in moto in un campo centrale dato.

Nel caso in cui l'interazione sia inversamente proporzionale al quadrato della distanza, come nel caso delle forze gravitazionali, integrando le equazioni del moto si ottiene l'equazione di una sezione conica. Se la traiettoria è aperta si ottiene, a secondo dell'energia del sistema, una traiettoria parabolica o iperbolica. Nel caso di traiettorie chiuse si ottiene invece un'orbita circolare (in corrispondenza del valore minimo del potenziale) o ellittica.

Le orbite ellittiche hanno grande importanza in meccanica celeste, essendo l'orbita circolare un caso particolare che difficilmente si realizza in natura, ma ricoprono un ruolo centrale anche in astronautica. Ad esempio il modo più efficiente (sotto certe condizioni) per passare da un'orbita circolare ad un'altra orbita circolare avente raggio differente consiste nell'accendere due volte i propulsori per entrare e poi uscire da un'orbita ellittica tangente ad entrambe le orbite circolari. Questo tipo di manovra si chiama trasferimento alla Hohmann, teorizzata dall'ingegnere tedesco Walter Hohmann nel 1925. L'esempio classico è il trasferimento in orbita geostazionaria, GTO (geostationary transfer orbit), in cui si passa da un'orbita bassa (LEO) ad un'orbita geostazionaria (GEO).

Propulsione aerospaziale

Per raggiungere le elevate velocità orbitali è necessario utilizzare un sistema di propulsione (dal verbo propellere, spingere innanzi). In un certo senso tutti i propulsori sono "a reazione", che siano essi terrestri, navali, aerei o spaziali. La forza propulsiva si ottiene infatti come reazione a una forza uguale e contraria applicata a sostanze solide (mezzi terrestri), liquide (mezzi navali) o gassose (mezzi aerei), che sono costituite del tutto o in parte dall'ambiente esterno (nei primi tre casi), o che sono trasportate interamente a bordo del mezzo (nel caso dei veicoli spaziali). Il termine propulsore a reazione viene però riservato normalmente a propulsori che espellono massa per ottenere la spinta.

Nel caso dei propulsori aerospaziali la forza propulsiva si ottiene incrementando la quantità di moto del fluido propulsivo. Questo può avvenire: all'esterno del veicolo, come nei propulsori a elica; all'interno, ma su fluidi in buona parte esterni, come negli esoreattori, in cui la maggior parte del fluido è costituito dall'atmosfera e la restante parte dal carburante trasportato internamente; o infine all'interno su fluidi interni, come negli endoreattori. Questi ultimi sono l'unica scelta possibile se si vuole che i propulsori operino nello spazio vuoto.

L'esempio più elementare di endoreattori è semplicemente un ugello collegato ad un serbatoio di gas inerte in pressione. Sistemi simili sono usati per il controllo dell'assetto in molti veicoli spaziali, impiego in cui non è necessario raggiungere spinte notevoli. Il passo successivo è aumentare la velocità del fluido espulso. Il metodo più diffuso, l'unico che permette di raggiungere spinte sufficienti per il decollo da terra, è attraverso un meccanismo termico. Si parla in questo caso di endoreattori termici. Altre possibilità possono essere sistemi elettrostatici o elettromagnetici che utilizzano come propellenti ioni o plasma, relegati a causa delle spinte ridotte alle manovre orbitali di satelliti e sonde. A sua volta il meccanismo termico può essere ottenuto in differenti modi, il più diffuso dei quali è quello chimico. Si parla in questo caso di endoreattori chimici. Altre possibilità possono essere l'utilizzo dell'energia solare o nucleare.

Gli endoreattori chimici si possono dividere in due categorie a seconda del fatto di essere alimentati a propellenti solidi o liquidi. Quelli a propellente solido hanno svariate caratteristiche positive. Sono più semplici (in sostanza sono costituiti semplicemente da un grano di propellente contenente una miscela di combustibile e ossidante in forma solida, un sistema di innesco e un ugello), sono facilmente scalabili (il progetto di un razzo più grande è in gran parte ricavabile riscalando il progetto di un razzo più piccolo, cosa impossibile per i più complessi sistemi a propellenti liquidi) e possono essere immagazzinati facilmente per lungo tempo (cosa che li rende particolarmente adatti per scopi militari). Di contro non permettono la regolazione della spinta, lo spegnimento prima dell'esaurimento del combustibile e la riaccensione, caratteristiche che li relega ad essere utilizzati in ambito spaziale come booster di supporto alla partenza. I più complessi sistemi a propulsori a propellente liquido sono costituiti da serbatoi separati per combustibile e ossidante, sono spesso dotati di turbopompe per aumentare il flusso di propellenti, una camera di combustione con un complesso sistemi di iniezione del propellente e infine l'ugello. La maggior complessità è largamente ripagata da maggiori prestazioni (grazie agli enormi flussi permessi dalle turbopompe), dalla modulabilità della spinta e dalla possibilità di spegnere e riaccenderli a piacimento.

Il modo più naturale di quantificare l'efficienza di un propulsore spaziale è indicare il rapporto tra la spinta $F$ e la portata di propellenti $\dot m$. La quantità risultante $F / \dot m$ ha la dimensione di una velocità, infatti $$ 1 \, \frac{\text{N}}{\text{kg} / \text{s}} = 1 \, \frac{\text{kg} \, \text{m}}{\text{s}^2} \frac{\text{s}}{\text{kg}} = 1 \, \frac{\text{m}}{\text{s}} $$ È però consuetudine indicare la spinta in massa equivalente (chilogrammi peso o libbre peso). Essendo $g_0 = 9.80665 \, \text{m} / \text{s}^2$ l'accelerazione standard di gravità la grandezza di riferimento, chiamata impulso specifico, è quindi $$ I_{sp} = \frac{F}{g_0 \, \dot m} $$ Il motivo che ha portato all'affermazione di questa definizione va cercato probabilmente nell'eterogeneità delle unità di misura utilizzate in ambito ingegneristico (soprattutto nei paesi anglosassoni, dove è ancora abbastanza comune utilizzare unità di misura non standard). Questa definizione ha infatti il pregio di essere del tutto indipendente dalle unità di misura usate per distanze, masse e forze. L'impulso specifico così definito ha la dimensione di un tempo e si indica in secondi, infatti $$ 1 \, \frac{\text{kg}}{\text{kg} / \text{s}} = 1 \, \frac{\text{kg} \, \text{s}}{\text{kg}} = 1 \, \text{s} $$

Conoscendo la spinta del propulsore e l'impulso specifico si può facilmente ricavare la portata di propellenti. Per i propulsori a propellente liquido poi, conoscendo il mixture ratio (rapporto tra ossidante e combustibile), si può di conseguenza calcolare il consumo di ossidante e combustibile del razzo.

Resistenza aerodinamica

L'equazione fondamentale per calcolare la forza dovuta alla resistenza aerodinamica del razzo è $$ F_d = \frac{1}{2} c_d \, A \, \rho \, v^2 $$ dove $c_d$ è il coefficiente di resistenza aerodinamica (adimensionale), $A$ è l'area di riferimento ($\text{m}^2$), $\rho$ è la densità dell'aria ($\text{kg} / \text{m}^3$) e $v^2$ è il quadrato della velocità relativa ($\text{m}^2 / \text{s}^2$). $c_d$ è un coefficiente che viene normalmente ricavato sperimentalmente. Attualmente utilizzo principalmente tre valori: $0,2$ per gli oggetti aerodinamici (carenature, ogive, eccetera), $2$ per i paracadute e $1$ per tutto il resto (scudi termici delle capsule, stadi in rientro atmosferico, eccetera). La densità dell'aria invece dipende dall'altitudine ed è calcolata secondo l'approssimazione data da: $$ \rho = \rho_0 \, e^{-\frac{h}{h_0}} $$ dove $\rho_0 = 1.225 \, \text{kg} / \text{m}^3$ è la densità atmosferica standard al livello del mare, $e$ è la costante di Nepero (vedi Argand.exe), $h$ è l'altitudine in metri e $h_0$ è un'altitudine di riferimento (circa $10 \, \text{km}$).

Il coefficiente $c_d$ e l'area $A$ dipendono dal razzo, mentre la parte restante dell'espressione ha la dimensione di una pressione ($\text{Pa}$, ovvero $\text{N} / \text{m}^2$) ed è chiamata pressione dinamica. L'intera espressione ha invece la dimensione di una forza, infatti $$ 1 \, \text{m}^2 \frac{\text{kg}}{\text{m}^3} \frac{\text{m}^2}{\text{s}^2} = 1 \, \text{kg} \, \frac{\text{m}}{\text{s}^2} = 1 \, \text{N} $$ ed è proprio la forza da applicare al razzo in direzione contraria alla velocità.

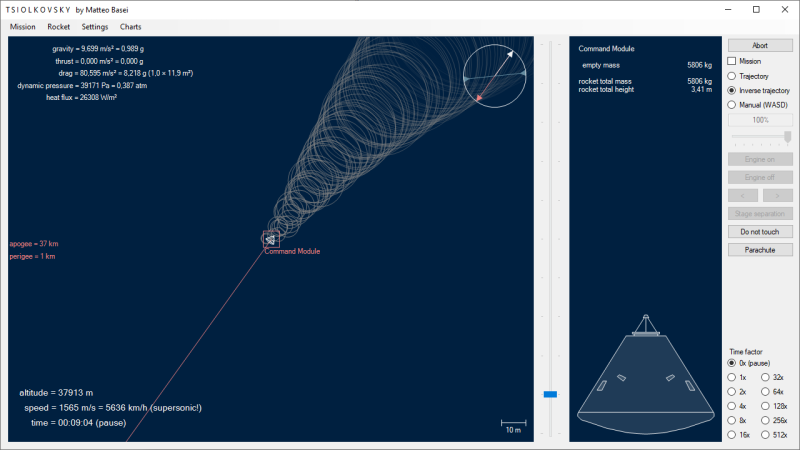
Shape editor

La grafica è volutamente essenziale, con sagome disegnate in bianco su blu che richiamano gli storici blueprint usati per i disegni tecnici prima dell'avvento dell'era digitale. È presente un editor che permette di disegnare le sagome posizionando i vertici sopra un'immagine di riferimento caricata e posizionata opportunamente.

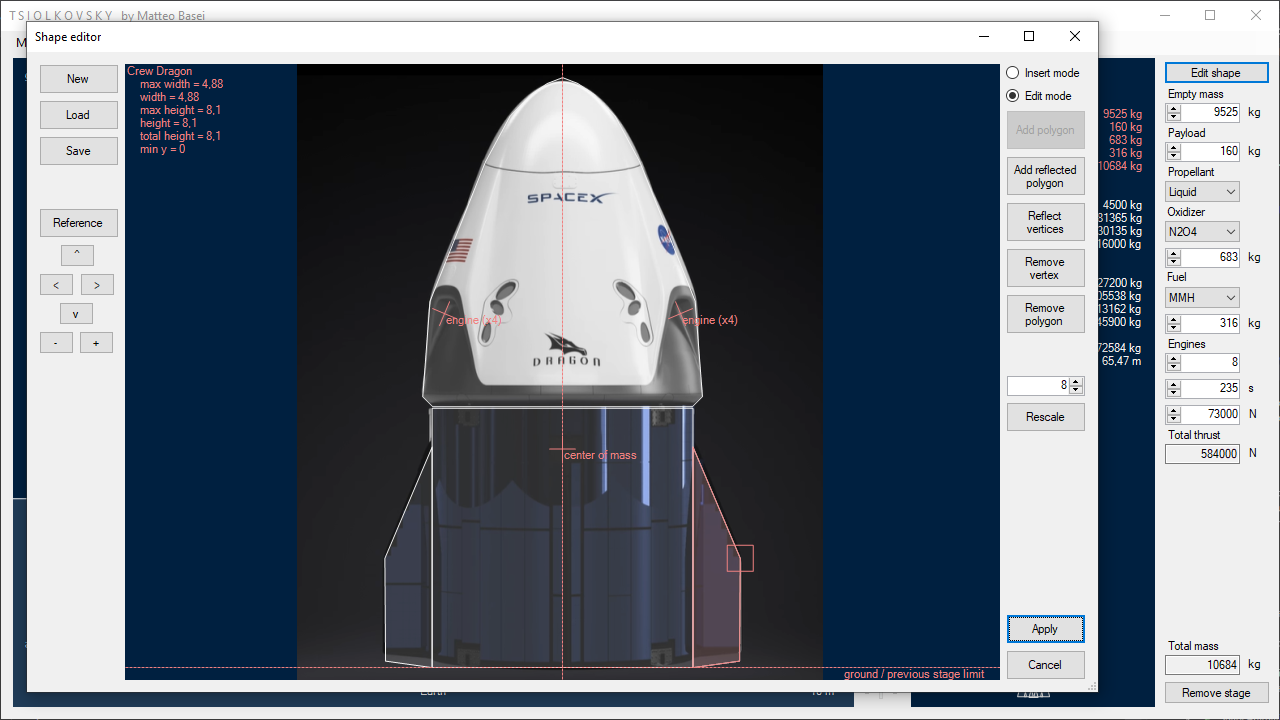
Grafici

Il programma permette di visualizzare in tempo reale, durante la simulazione, i grafici di altitudine, velocità, accelerazione e pressione dinamica del razzo.

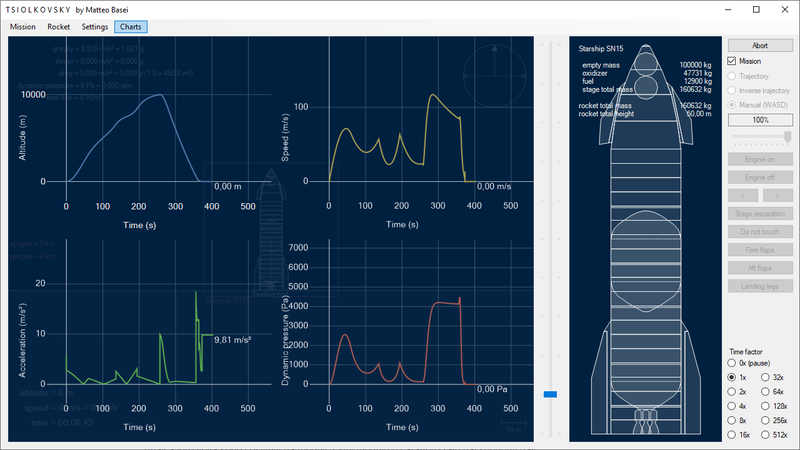
Archivio veicoli

La struttura e i dati dei razzi possono essere salvati e caricati su file JSON. Ogni razzo è costituito da stadi, i quali a loro volta sono costituiti da moduli. Ogni modulo è caratterizzato dai seguenti dati:

• name
• emptyMass ($\text{kg}$)
• payload ($\text{kg}$)
• solidPropellantType
• solidPropellantMass ($\text{kg}$)
• oxidizerType
• oxidizerMass ($\text{kg}$)
• fuelType
• fuelMass ($\text{kg}$)
• externalTank
• engineCount
• thrust ($\text{N}$)
• propellantFlow ($\text{kg} / \text{s}$)
• hasThrustControl (boolean)
• hasGimbaledOrVernierThruster (boolean)
• shape (lista di coordinate in $\text{m}$)
• centerOfMassX ($\text{m}$)
• centerOfMassY ($\text{m}$)
• dragCoefficient (adimensionale)
• dragArea ($\text{m}^2$)
• hasHeatShield (boolean)
• isLateral (boolean)
• separationRoll ($\text{rad} / \text{s}$)
• separationLateralSpeed ($\text{m} / \text{s}$)
• mission (lambda function)

"hasHeatShield" indica se il modulo è dotato di scudo termico e in pratica incrementa i $\text{W} / \text{m}^2$ di flusso di calore sopportabili dal modulo prima di esplodere. "isLateral" indica invece se il modulo è posto lateralmente rispetto al resto del razzo, quindi in pratica se calcolare la forza di resistenza aerodinamica anche quando il modulo non è nell'ultimo stadio del razzo. Ogni stadio, oltre al nome e alla lista dei moduli, è caratterizzato da una serie di booleani:

• name
• isFairing (boolean)
• isNosecone (boolean)
• isManually (boolean)
• isSynchronizedWithNext (boolean)
• modules (lista dei moduli)

"isFairing" indica che lo stadio è una carenatura, quindi che gli stadi successivi saranno al suo interno. "isNosecone" indica che la carenatura è un'ogiva, e quindi che per il calcolo della resistenza aerodinamica bisogna considerare tale stadio e ignorare i successivi. "isManually" indica che lo stadio non si attiva automaticamente alla separazione con lo stadio precedente ed è usato ad esempio per le navicelle i cui propulsori servono per il deorbit. Infine "isSynchronizedWithNext" indica che lo stadio si accende insieme allo stadio successivo, tipicamente per alcuni razzi che alla partenza accendono contemporaneamente primo stadio e booster. Infine il razzo:

• name
• manufacturer
• description
• imagePath
• videoLink
• mission (lambda function)
• pointsOfInterest (lista di nomi e coordinate in $\text{m}$)
• stages (lista degli stadi)

"pointsOfInterest" è una serie di punti di interesse con relativa etichetta, ad esempio la posizione delle drone ship per le missioni dei Falcon 9 di SpaceX. "mission" è uno script di missione che consiste in pratica in una serie di azioni sincronizzate con il tempo dal lancio. Può essere regolata la direzione, la spinta dei propulsori, la separazione degli stadi e tutte le altre funzionalità accessibili dall'interfaccia.

Gli script di missione possono essere assegnati anche a livello del singolo modulo. Al lancio viene eseguito lo script del razzo, che resterà attivo fino al termine della missione per l'ultimo stadio. Gli script degli stadi inferiori resteranno invece inattivi fino alle rispettive separazioni. In questo modo è possibile ad esempio assegnare uno script ai booster del Falcon 9, con le azioni da compiere per il rientro e l'atterraggio propulsivo.

Questi sono i principali veicoli che ho scelto di simulare durante lo sviluppo della simulazione.

Lanciatori R-7

I lanciatori sovietici della famiglia R-7 sono tra i più straordinari e importanti razzi nella storia dell'astronautica. Sono stati i più utilizzati e i più affidabili vettori spaziali mai costruiti.

Il capostipite è stato il primo missile balistico intercontinentale e le successive versioni hanno raggiunto molti altri importanti primati. Hanno portato in orbita lo Sputnik nel 1957, il primo satellite artificiale, la Vostok, che ha portato il primo uomo nello spazio (Jurij Gagarin) nel 1961 e la Voschod, dalla quale è stata eseguita la prima passeggiata spaziale nel 1965.

Sono tutt'oggi in servizio, in versioni migliorate e ammodernate, come lanciatori della navicella Soyuz, che dalla dismissione dello Space Shuttle nel 2011 e fino all'entrata in servizio della Crew Dragon di SpaceX nel 2020 è stata l'unico modo per portare gli astronauti sulla ISS.

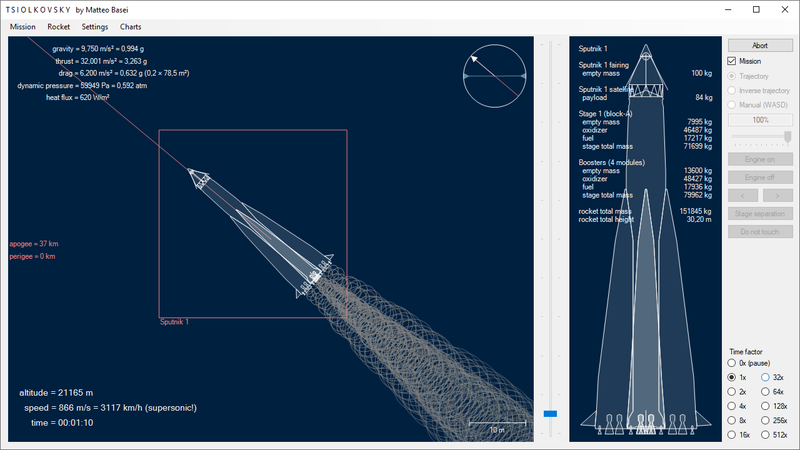
Lanciatori Titan

Anche la famiglia di vettori Titan, come molti altri razzi spaziali, trae origine da un missile balistico intercontinentale. Il Titan II è stato il vettore delle capsule Gemini, chiamato in questa versione Titan GLV (Gemini Launch Vehicle). Il programma Gemini, insieme al programma Mercury, è stato uno dei passi nella corsa allo spazio statunitense, culminata con il programma Apollo e lo sbarco dell'uomo sulla Luna.

Il Titan IIIE (con il Centaur D-1T come terzo stadio) è stato invece il vettore delle sonde Voyager, le prime sonde ad esplorare il sistema solare esterno. La Voyager 2 è ad oggi (2020) l'unica sonda ad aver effettuato un passaggio ravvicinato di Urano e Nettuno ed entrambe, ancora funzionanti dopo più di quarant'anni, sono gli unici manufatti umani ad aver superato l'eliopausa ed essere quindi usciti dal sistema solare. Questo sistema di lancio è stato particolarmente importante nello sviluppo della mia simulazione, avendone trovato un'approfondita descrizione (un documento del settembre 1973, redatto per la NASA dalla General Dynamics e dalla Martin Marietta, produttori rispettivamente del Centaur D-1T e del Titan IIIE) ed essendo un vettore estremamente articolato.

È infatti provvisto di due booster in tandem a combustibile solido (stadio 0) e due stadi a propellenti liquidi, sormontati da una carenatura. I due stadi sono alimentati a tetrossido di diazoto (N₂O₄), come ossidante, e Aerozina 50 come combustibile. L'Aerozina 50 è una miscela 50/50 di idrazina (N₂H₄) e dimetilidrazina asimmetrica (C₂N₂H₈, sigla UDMH), un composto appositamente sviluppato per il Titan che è più stabile rispetto all'idrazina pura e più denso rispetto alla dimetilidrazina asimmetrica pura. La carenatura contiene il terzo stadio (il Centaur a idrogeno e ossigeno liquidi), l'apogee kick motor a combustibile solido Star 37E e infine la sonda Voyager.

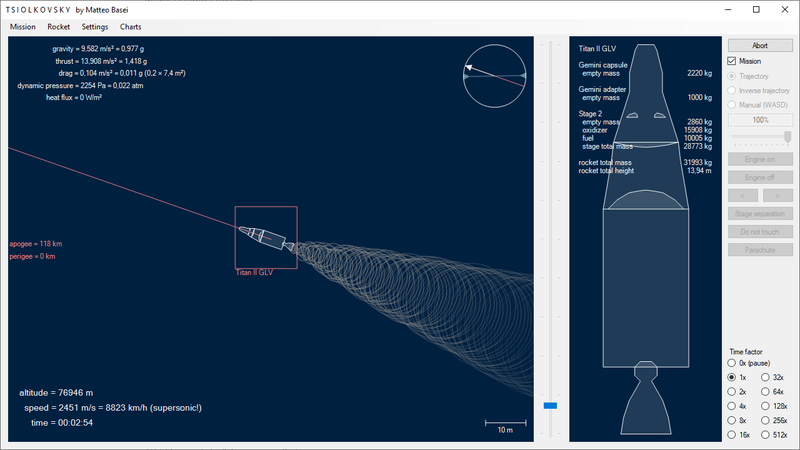
Saturn V

Non poteva mancare il Saturn V, il vettore del programma Apollo, che ha portato l'uomo sulla Luna, nonché il più grande e potente razzo mai costruito dall'uomo (al 2021, anche se sono in arrivo l'SLS della NASA e la Starship di SpaceX). Unico razzo ad aver portato l'uomo su un altro corpo celeste, tra il 16 luglio 1969 e il 1972 ha portato 12 uomini sulla Luna.

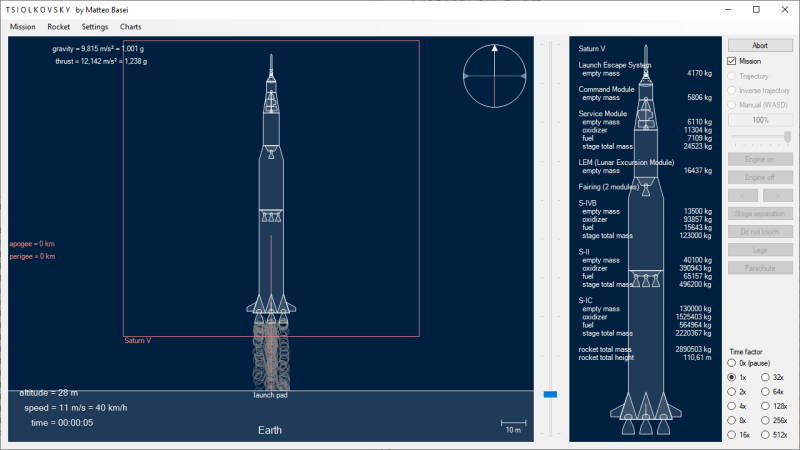
Space Shuttle e Space Launch System

Lo Space Shuttle è il sistema di lancio che ha richiesto il maggior numero di modifiche al mio simulatore, modifiche che oltretutto non sono utilizzate in nessun altro razzo presente nella simulazione (e, per quanto ne so, esistente). È infatti un lanciatore estremamente anomalo. È l'unico in cui un modulo, l'orbiter, attinge il propellente da un altro modulo, l'external tank. È inoltre l'unico ad essere asimmetrico e in cui quindi l'asse verticale in cui giace il baricentro non corrisponde all'asse in cui giace il centro geometrico. Inoltre i propulsori principali, gli RS-25, spingono in direzione non verticale (e in modo asimmetrico, come invece succede ad esempio per i booster del Titan IIIE).

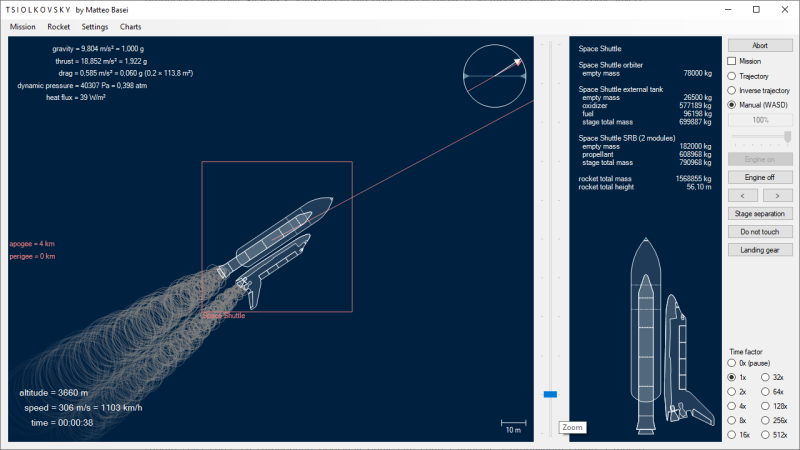
Dalle ceneri del progetto Space Shuttle, che ha completato il suo ultimo volo il 21 luglio 2011, nasce lo Space Launch System (SLS), destinato a riportare l'uomo sulla Luna e successivamente su Marte. L'SLS è una specie di mostro di Frankenstein che riutilizza varie componenti e progetti dello Space Shuttle e le ripropone in una forma più classica e vicina ad un razzo come il Saturn V, che portò per la prima volta l'uomo sulla Luna. Le componenti principali riutilizzate sono i booster a propellente solido, i motori principali, gli RS-25, che ora trovano una collocazione più classica sotto il serbatoio principale, che viene progettato a partire dal serbatoio esterno dello Shuttle. Il secondo stadio...

SpaceX

SpaceX viene fondata nel 2002 da Elon Musk con i soldi ricavati dalla vendita di PayPal. Lo spunto per iniziare questa nuova e insolita attività imprenditoriale deriva dalla frequentazione da parte di Musk della Mars Society, organizzazione che cerca di promuovere l'esplorazione di Marte. I tentativi falliti di trovare un vettore economico per portare piccoli carichi su Marte spingono Musk a decidere di sviluppare il proprio sistema di lancio.

Il primo razzo sviluppato dall'azienda è il Falcon 1 che il 28 settembre 2008, dopo tre tentativi falliti tra il 2006 e il 2008, si aggiudica il primato di essere il primo razzo privato ad effettuare un volo orbitale. Dopo solo 2 voli viene abbandonato (come pure il successore Falcon 5, previsto, ma mai sviluppato). Questo razzo a due stadi monta un motore Merlin nel primo stadio e un Kestrel nel secondo. Entrambi sviluppati da SpaceX stessa (secondo il principio per cui la frammentazione della produzione che caratterizza l'industria aerospaziale sia una delle cause dei lunghi tempi di sviluppo e dei costi proibitivi), sono due classici motori a LOX / RP-1. Il secondo, più semplice, è privo di turbopompe (l'alimentazione è quindi assicurata solo dalla pressione dei serbatoi), utilizza un sistema di raffreddamento ablativo per l'ugello e raggiunge i 35 kN di spinta. Il Merlin è invece dotato di turbopompe azionate da un'unica turbina secondo il classico schema del ciclo a generazione di gas. Nella sua terza versione è dotato anche di ugello a raffreddamento rigenerativo in cui il cherosene prima di essere iniettato in camera di combustione viene utilizzato per raffreddare l'ugello. Nelle prime versioni montate sul Falcon 1 produce 340 kN di spinta, per poi arrivare nelle sue ultime versioni a raggiungere ben 850 kN.

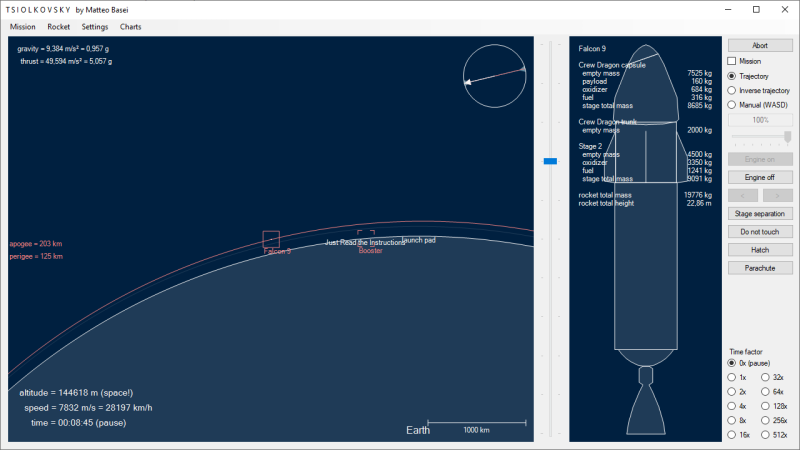
Annullato lo sviluppo del Falcon 5, versione che doveva ospitare nel primo stadio 5 motori Merlin, SpaceX passa direttamente allo sviluppo del Falcon 9, che compie i suoi primi lanci già nel 2010. Rispetto al Falcon 1 monta un motore Merlin, ottimizzato per il vuoto, anche nel secondo stadio e ne monta ben 9 nel primo. Ma la vera novità che contraddistingue questo nuovo razzo sarà introdotta solo successivamente. Parallelamente viene infatti sviluppato il Grasshopper, dimostratore tecnologico che effettua 8 "balzi" tra il 2012 e il 2013. È il banco di prova che permetterà di rendere riutilizzabile, grazie alla capacità di atterraggio propulsivo, i primi stadi della SpaceX. Il primo atterraggio del primo stadio del Falcon 9, nonché primo atterraggio propulsivo assoluto per il primo stadio di un razzo orbitale, avviene il 21 dicembre 2015.

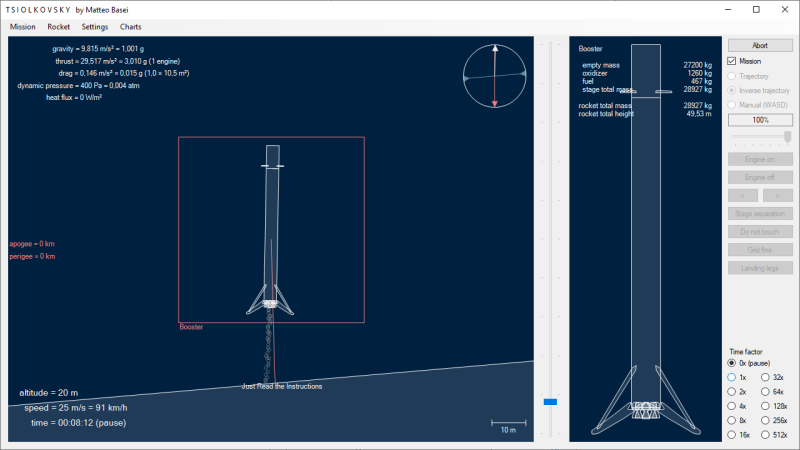
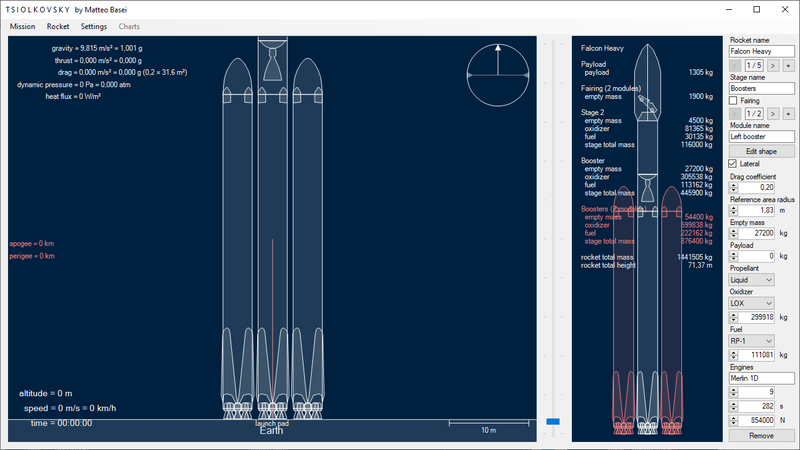
Il Falcon Heavy consiste in sostanza in un Falcon 9 a cui sono collegati altri due primi stadi dello stesso vettore modificati allo scopo (la stessa configurazione del Delta IV Heavy della Boeing). Il primo lancio è stato effettuato il 6 febbraio del 2018 collocando una Tesla Roadster in orbita eliocentrica.

SpaceX oltre al sistema di lancio Falcon sviluppa anche le capsule riutilizzabili Dragon. La prima versione, in attività dal 2010 al 2020, viene utilizzata per rifornire la Stazione Spaziale Internazionale. La seconda versione è disponibile in due versioni denominate Cargo Dragon e Crew Dragon, la prima per rimpiazzare la vecchia versione per il trasporto merci e la seconda con equipaggio. Il 30 maggio 2020 effettua il suo primo lancio con a bordo due astronauti.

Le capsule Dragon montano i motori Draco per il controllo dell'assetto. Sono piccoli motori a combustibile liquido ipergolico sviluppati da SpaceX. Alimentati da monometilidrazina (CH₆N₂) e tetrossido di diazoto (N₂O₄) come ossidante, sviluppano una spinta di 400 newton. Una loro evoluzione ben 200 volte più potente, chiamata SuperDraco, è montata sulla capsula Crew Dragon per il sistema di aborto del lancio (e ipoteticamente per un eventuale atterraggio propulsivo, sistema attualmente abbandonato).

Lo Starhopper è il dimostratore tecnologico per il nuovo veicolo di SpaceX, la Starship, che si pone l'ambizioso obiettivo di colonizzare Marte. Monta un singolo motore Raptor, il nuovo propulsore sviluppato dalla SpaceX, ed effettua un "salto" di 150 metri il 27 agosto 2019. Il Raptor ha due caratteristiche abbastanza innovative nell'ambito della propulsione aerospaziale. Per prima cosa utilizza come combustibile il metano (CH₄), propellente scelto per il fatto di essere un buon compromesso tra il cherosene e l'idrogeno (in fatto di densità, efficienza, punto di ebollizione, temperatura di combustione e complessità della reazione), e per il fatto di essere teoricamente producibile su Marte. Inoltre il Raptor utilizza un ciclo più efficiente di quello a generazione di gas, chiamato a "flusso completo". Mentre nel sistema a generazione di gas la precombustione che alimenta la turbina delle turbopompe è "a perdere", con scarico separato, nel sistema a flusso completo la precombustione è integrata nel sistema di alimentazione. In questo modo i due flussi in uscita dai precombustori (uno con prevalenza di combustibile, l'altro con prevalenza di ossidante) permettono di mantenere relativamente bassa la temperatura nelle turbine e in camera di combustione, per il fatto di essere due flussi di gas caldi, migliorano la miscelazione e di conseguenza aumentano l'efficienza della reazione.

La Starship è un enorme secondo stadio completamente riutilizzabile del diametro di 9 metri ed alta 50 metri. È costruita interamente in acciaio, materiale che per il peso notevole non viene molto utilizzato in ambito aerospaziale come materiale principale. Rispetto a molti altri materiali più leggeri però si comporta molto bene sia alle basse temperature richieste dallo stoccaggio dei propellenti criogenici, sia alle alte temperature sviluppate dall'attrito atmosferico in fase di rientro. Inoltre è molto più economico e facile da lavorare, cosa che si sposa bene con la filosofia di lavoro di SpaceX, caratterizzata da continue iterazioni di progettazione, sviluppo e test.

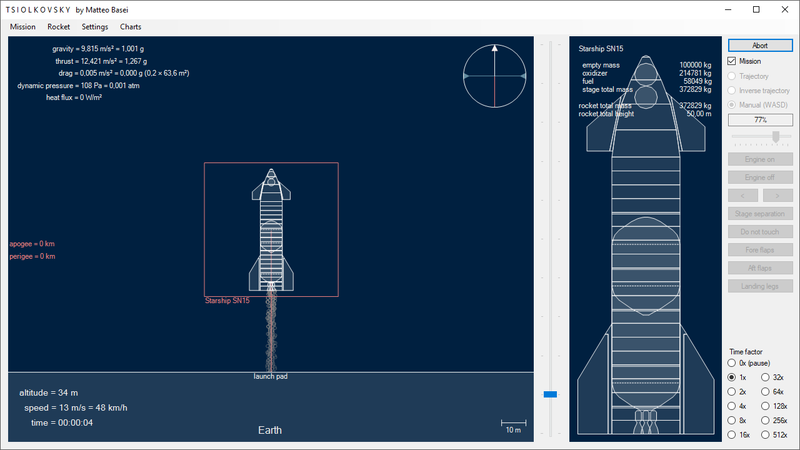
Il 4 agosto 2020 il prototipo chiamato SN5 (serial number 5), costituito in sostanza dalla sola sezione dei serbatoi e motori (per un totale di circa 30 metri di altezza) effettua con successo il primo "salto" di 150 metri, seguito a breve dall'SN6. L'SN8 è invece il primo prototipo con ogiva, superfici aerodinamiche e la configurazione completa di 3 Raptor atmosferici (il numero finale di motori previsto è 3 atmosferici e 3 ottimizzati per il vuoto). Effettua con successo il primo volo subsonico e suborbitale il 9 dicembre 2020, compiendo correttamente la salita fino a 12,5 chilometri, la caduta controllata tramite le superfici aerodinamiche e il ritorno in assetto verticale. Esplode al momento dell'atterraggio a causa di un problema di pressione da un serbatoio. Il 2 febbraio 2021 stessa sorte tocca all'SN9, questa volta per la mancata accensione di uno dei due motori durante l'ultima fase. L'SN10 effettua il primo atterraggio, anche se non proprio morbidissimo ed esplode poco dopo a causa dei danni subiti mentre l'SN11 esplode in volo poco prima di effettuare la manovra di atterraggio per motivi non del tutto chiariti. I prototipi 12, 13 e 14 vengono annullati e tocca infine all'SN15 effettuare un atterraggio perfetto il 5 maggio 2021.