Verhulst.exe il caos da un modello demografico

"Il battito d'ala di una farfalla a Rio de Janeiro, amplificato dalle correnti atmosferiche, potrebbe causare un tornado in Texas due settimane dopo."

Pierre Francois Verhulst è stato un matematico belga noto per aver formulato nel 1838 l'equazione logistica, la cui versione a tempo discreto, detta mappa logistica, è semplicemente $$ x_{n + 1} = r \, x_n \left( 1 - x_n \right) $$ dove $r$ è il tasso di crescita e $0 \lt x_0 \lt 1$. Questa relazione di ricorrenza, resa popolare nel 1976 da Robert May, fornisce un modello demografico, quindi $x_n$ va interpretato come un numero proporzionale alla popolazione all'$n$-esima generazione. La cosa interessante è che questa semplice formula per $3,57 \lt r \lt 4$ fornisce un notevole esempio di comportamento caotico.

Rappresentazione della mappa logistica

Questo programma mostra il diagramma delle biforcazioni della mappa logistica che a causa del comportamento caotico di quest'ultima è un frattale (se ti interessasse approfondire la connessione tra comportamenti caotici e frattali potresti leggere questa pagina, mentre per una definizione generale di frattale puoi dare un'occhiata a quest'altra). Il diagramma delle biforcazioni è un grafico che ha in ascissa il valore di $r$ e in ordinata i valori di $x_n$ generazione dopo generazione.

Per ottenere un'immagine gradevole nelle regioni caotiche del grafico, per ogni colonna di pixel (quindi per ogni valore di $r$ considerato) viene contato il numero di volte in cui $x_n$ cade in un determinato pixel della colonna e poi in base al rapporto tra questo numero e il numero totale di iterazioni effettuate viene associata ad ogni pixel una certa tonalità di grigio.

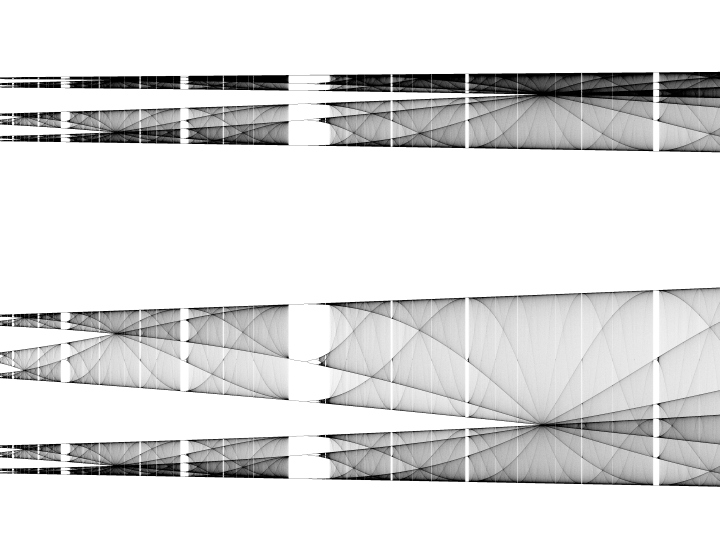
Comportamento al variare di $r$

Per valori di $r$ minori di $1$ la popolazione crolla a $0$ molto velocemente. Per valori compresi tra $1$ e $3$ la popolazione si stabilizza in un unico valore. Oltre $r = 3$ si ha la prima biforcazione, la popolazione inizia ad oscillare continuamente tra due valori. Andando oltre si ha una successiva biforcazione intorno a $r \approx 3,45$ che porta i valori a $4$, poi $8$, eccetera. Superando $r \approx 3,57$ inizia la fase caotica in cui la popolazione oscilla in modo incontrollato. Superato $r = 4$ il valore di $x_n$ esce dall'intervallo $\left[ 0 , 1 \right]$.

Altre relazioni di ricorrenza

La mappa logistica non è l'unica relazione di ricorrenza che mostra un comportamento caotico ed è molto interessante notare come molte altre formule permettano di ottenere immagini simili a quelle ottenibili con la mappa logistica. Ad esempio la formula $$ x_{n + 1} = r \, \cos(x_n) $$

Un'altra interessante relazione di ricorrenza è quella che definisce l'insieme di Mandelbrot, che è definito come l'insieme dei punti $c$ del piano complesso in cui la successione $$ \begin{alignedat}{2} z_0 &= 0 \\ z_{n + 1} &= z_n^2 + c \end{alignedat} $$ è limitata. L'intersezione tra l'insieme di Mandelbrot e l'asse reale è l'intervallo $\left[ -2 , 1 / 4 \right]$, quindi il diagramma delle biforcazioni di $$ x_{n + 1} = x_n^2 + r $$ per $-2 < r < 1 /4$ può essere messo in relazione con l'insieme di Mandelbrot.

Utilizzando un programma che mostri, oltre all'insieme di Mandelbrot, il comportamento della successione per un punto dato (come questo mio programma), è possibile verificare facilmente il numero di valori tra cui la successione oscilla a seconda della posizione di $c$ nel piano complesso.

Altri collegamenti

L'equazione logistica originariamente studiata da Verhulst, cioè la versione continua della mappa logistica $$ \frac{d}{dx} f(x) = f(x) \left( 1 - f(x) \right) $$ ha come soluzioni la funzione logistica $$ f(x) = \frac{1}{1 + e^{-x}} $$ che è una delle più comuni funzioni sigmoidee.

Queste (e altre, come la tangente iperbolica) funzioni vengono usate nelle reti neurali come funzioni di attivazione, in quanto sono una sorta di versione differenziabile della funzione a gradino di Heaviside (vedi questa pagina, che spiega l'algoritmo di apprendimento delle reti neurali, per capire la necessità di utilizzare funzioni differenziabili come funzioni di attivazione nelle reti neurali).