VonMangoldt.exe la musica dei numeri primi

"C'è una cosa di cui i non matematici non si rendono conto: la matematica è in realtà quasi interamente un soggetto estetico."

Il legame tra gli zeri della funzione zeta di Riemann e la distribuzione dei numeri primi è uno degli argomenti più affascinanti della matematica pura. Lo scopo di questo piccolo programma è quello di farvi intravvedere la bellezza di questo argomento, dandovi un'idea intuitiva del fatto che gli zeri non banali della funzione zeta di Riemann diventano delle note, che suonate contemporaneamente, in una sorta di accordo infinito, ci suonano la distribuzione dei numeri primi.

Per poter apprezzare il senso di questo programma, che di per sé non fa altro che tracciare un paio di grafici, c'è bisogno di un po' di spiegazioni, quindi partiamo dal principio...

I numeri primi

La teoria dei numeri è la branca della matematica che si occupa dello studio dei numeri interi. I metodi utilizzati provengono spesso dai più svariati campi della matematica, anche molto avanzati, ma il soggetto dello studio è relativamente semplice, tanto che molti problemi della teoria dei numeri possono essere definiti in termini comprensibili a chiunque. Nonostante ciò la loro soluzione è spesso tutt'altro che banale, e in molti casi delle congetture apparentemente vere resistono indimostrate per centinaia di anni.

Uno degli esempi più celebri è l'ultimo teorema di Fermat riguardante le equazioni diofantee, equazioni a coefficienti interi di cui si ricercano le soluzioni intere, che costituiscono uno degli argomenti centrali della teoria dei numeri. Tale teorema afferma che non esistono soluzione intere positive per l'equazione $$ a^n + b^n = c^n $$ se $n > 2$ (per $n = 2$ le soluzioni, infinite, sono le famose terne pitagoriche). Tale enunciato, formulato da Pierre de Fermat nel lontano 1637, è stato dimostrato solo nel 1995 da Andrew Wiles, utilizzando metodi sofisticati della matematica moderna e in particolare della geometria algebrica, della teoria di Galois, delle curve ellittiche e delle forme modulari.

Nella teoria dei numeri i numeri primi occupano un posto speciale. Anche in questo caso, i numeri primi possono essere definiti in modo estremamente semplice: sono gli interi che possiedono esattamente due divisori distinti, se stessi e l'unità. La sequenza inizia con $$ 2 , 3 , 5 , 7 , 11 , 13 , ... $$ Nonostante la definizione estremamente semplice e il loro ruolo fondamentale, essendo in un certo senso i "mattoni" fondamentali con cui sono costruiti gli interi (da un punto di vista moltiplicativo), è stato ben presto chiaro come la sequenza esatta in cui compaiono sia del tutto indecifrabile.

Il metodo classico per l'individuazione dei numeri primi è il Crivello di Eratostene (vedi PrimeColumns) in cui per stabilire se un certo intero $n$ è primo bisogna passare in rassegna tutti i numeri inferiori a $\sqrt{n}$ (una volta superata $\sqrt{n}$ gli ipotetici fattori di $n$ maggiori di $1$, che devono essere almeno $2$ perché $n$ non sia primo, darebbero come prodotto un numero maggiore di $n$, il che è assurdo). Metodi più avanzati introdotti successivamente migliorano le prestazioni, ma la sostanza resta la stessa: per determinare la sequenza dei numeri primi bisogna verificare la primalità di tutti gli interi in sequenza, operazione che diventa molto rapidamente computazionalmente ingestibile.

Le funzioni di enumerazione dei numeri primi

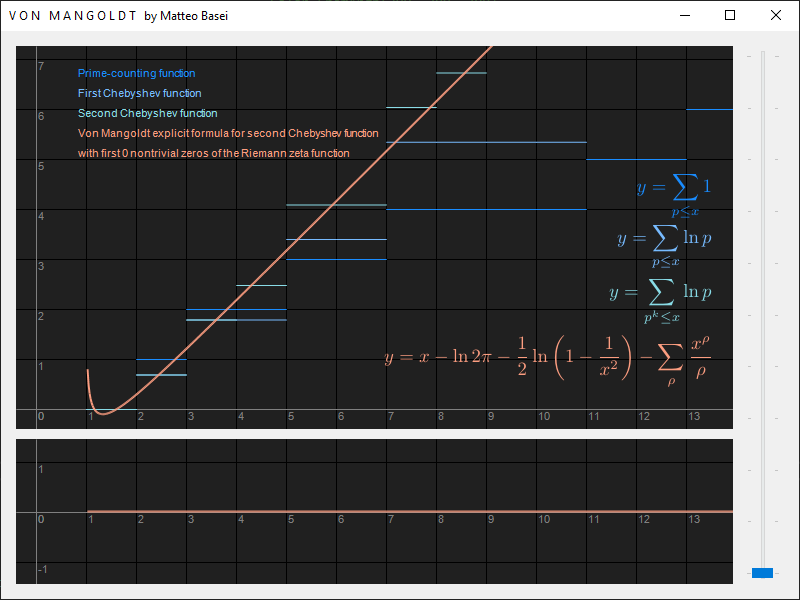
Vista l'apparente impossibilità di trovare un ordine nella distribuzione dei numeri primi il loro studio deviò, in particolare grazie ai lavori di Dirichlet e Chebyshev, verso lo studio delle loro comportamento asintotico e in particolare del comportamento della funzione enumerativa dei primi $\pi(n)$ che indica il numero di primi minori o uguali a $n$. In teoria analitica dei numeri, la branca della teoria dei numeri che utilizza i metodi dell'analisi, questa funzione viene studiata come funzione reale a variabile reale $\pi(x)$. Questa è la prima funzione disegnata dal programma, in blu, in formula $$ \pi(x) = \sum_{p \leq x} 1 $$ (dove si intende che la sommatoria sia estesa a tutti i numeri primi $p$ minori o uguali a $x$).

La prima funzione di Chebyshev, in azzurro, è una sua versione pesata $$ \vartheta(x) = \sum_{p \leq x} \ln p = \ln \left( \prod_{p \leq x} p \right) $$ dove quindi per ogni primo minore o uguale a $x$ invece di sommare $1$ sommiamo il logaritmo naturale del valore (il che equivale, per le note proprietà dei logaritmi, a prendere il logaritmo naturale del prodotto di ogni primo minore o uguale a $x$). Il senso di questa versione pesata è che i numeri primi diventano via via meno densi mano a mano che aumenta $x$. In particolare, come dimostrato dal cosiddetto teorema dei numeri primi, la funzione di enumerazione dei numeri primi $\pi(x)$ è asintotica a $x / \ln \left( x \right)$, cioè il limite per $x$ che tende ad infinito del rapporto tra le due funzioni tende a $1$ $$ \pi(x) \sim \frac{x}{\ln x} $$

Infine la seconda funzione di Chebyshev a differenza della prima conta le potenze dei primi minori o uguali a $x$ $$ \psi(x) = \sum_{k \in \mathbb{N}^+} \sum_{p^k \leq x} \ln p $$ Come vedremo grazie a questa funzione è possibile mostrare in modo diretto il legame tra la distribuzione dei numeri primi e gli zeri della funzione zeta di Riemann.

Questo legame è dato infatti dalla cosiddetta formula esplicita della seconda funzione di Chebyshev. Questa formula è stata dimostrata nel 1895 da Hans Carl Friedrich von Mangoldt, da cui il nome del programma, ma trae origine dal fondamentale articolo "Sul numero di numeri primi al di sotto di una certa grandezza" pubblicato nel 1859 da Bernhard Riemann, in cui il grande matematico introduce lo studio della funzione che ora porta il suo nome, rivoluzionando la teoria dei numeri. Tra le altre cose, è incredibile anche il fatto che questo articolo, di appena nove pagine, fu l'unico articolo di teoria dei numeri pubblicato da Riemann nella sua carriera.

Il prodotto di Eulero

La storia della funzione zeta inizia però con Eulero, che nel 1737 scoprì che $$ \sum \frac{1}{n^x} = \prod \frac{1}{1 - \frac{1}{p^x}} $$ dove $n \in \mathbb{N}^+$ (gli interi positivi, vale a dire l'insieme dei numeri naturali privati dello zero), $p \in \mathbb{P}$ (l'insieme dei numeri primi) e $1 < x \in \mathbb{R}$ (i numeri reali). Il secondo membro è chiamato prodotto di Eulero. La straordinarietà di questa identità stà nel fatto che lega una semplice e regolare sommatoria sugli interi positivi ad una imprevedibile produttoria sui numeri primi.

La dimostrazione di questa uguaglianza è estremamente semplice ed elegante. Indichiamo con $\zeta$ il primo membro $$ \zeta = \frac{1}{1^x} + \frac{1}{2^x} + \frac{1}{3^x} + ... $$ Moltiplicando ambo i membri per il secondo termine del secondo membro, cioè $1 / 2^x$, si ha $$ \frac{1}{2^x} \zeta = \frac{1}{2^x} + \frac{1}{4^x} + \frac{1}{6^x} + ... $$ dove nei denominatori dei termini del secondo membro compaiono ora tutte e solo le potenze dei multipli di $2$. Sottraendo membro e membro l'ultima alla penultima si ha $$ \left( 1 - \frac{1}{2^x} \right) \zeta = \frac{1}{1^x} + \frac{1}{3^x} + \frac{1}{5^x} + ... $$ dove in pratica abbiamo quindi eliminato a secondo membro tutti i termini in cui compariva a denominatore la potenza di un multiplo di $2$ e fatto comparire a primo membro un termine contenente una potenza di $2$.

Moltiplicando ancora ambo i membri per il secondo termine del secondo membro, questa volta $1 / 3^x$, si ha $$ \frac{1}{3^x} \left( 1 - \frac{1}{2^x} \right) \zeta = \frac{1}{3^x} + \frac{1}{9^x} + \frac{1}{15^x} + ... $$ dove ora nei denominatori dei termini del secondo membro compaiono tutte e solo le potenze dei multipli di $3$ che non siano anche multipli di $2$ (avendo già escluso i termini di questo tipo nel passaggio precedente). Sottraendo membro a membro l'ultima alla penultima otteniamo $$ \left( 1 - \frac{1}{3^x} \right) \left( 1 - \frac{1}{2^x} \right) \zeta = \frac{1}{1^x} + \frac{1}{5^x} + \frac{1}{7^x} + ... $$ In questo secondo passaggio abbiamo eliminato a secondo membro tutti i termini in cui compariva a denominatore la potenza di un multiplo di $3$ (che non erano già stati eliminati in quanto multipli di $2$) e fatto comparire a primo membro un termine contenente una potenza di $3$.

Un ulteriore passaggio eliminerebbe a secondo membro tutti i termini in cui a denominatore compare la potenza di un multiplo di $5$, poi si passerebbe al $7$, all'$11$, $13$, eccetera, un passaggio per ogni numero che non sia già stato eliminato in quanto multiplo di un numero già spostato a primo membro. In altre parole un passaggio per ogni numero primo. Eseguendo infiniti passaggi, moltiplicando ogni volta ambo i membri per il secondo termine del secondo membro e poi sottraendo membro a membro l'espressione ottenuta alla precedente, si eliminano tutti i multipli di tutti gli interi positivi e a secondo membro rimane $1 / 1^x$ ($= 1$). Alla fine si ottiene quindi $$ ... \left( 1 - \frac{1}{5^x} \right) \left( 1 - \frac{1}{3^x} \right) \left( 1 - \frac{1}{2^x} \right) \zeta = 1 $$ dove a primo membro compaiono tutti e solo i numeri primi. Quindi $$ \zeta = \prod \frac{1}{1 - \frac{1}{p^x}} $$ come volevasi dimostrare.

La funzione zeta di Riemann

La funzione zeta di Riemann è il prolungamento analitico della serie $\sum \frac{1}{n^x}$. È quindi una funzione complessa a variabile complessa (che ho disegnato, tra le altre, con il mio programma ImMap). Se non sai cosa siano i numeri complessi, prima di continuare la lettura di questa pagina, potresti dare un'occhiata al mio programma Argand.exe. Il prolungamento analitico è una tra le caratteristiche che rendono quasi "magici" i numeri complessi, ma la sua definizione è semplice: nel campo complesso quando una funzione analitica $f$ definita in un certo dominio $U$ prende gli stessi valori di un'altra funzione analitica $g$ in un sottoinsieme $V \subset U$ diciamo che $f$ è il prolungamento analitico di $g$. Il senso di questa definizione sta nel fatto che quando ciò è possibile, cioè quando le due funzioni coincidono in $V$, il prolungamento è unico.

La funzione zeta di Riemann può essere prolungata analiticamente a tutto il piano complesso ad esclusione del singolo punto $1$. Nel piano essa ha due tipologie di zeri (i punti in cui si annulla sia la parte reale che la parte immaginaria della funzione). I primi sono gli interi pari negativi, detti zeri banali, che derivano direttamente dal fatto che tale funzione soddisfa l'equazione funzionale $$ \zeta(z) = 2^z \pi^{z - 1} \sin \left( \frac{\pi z}{2} \right) \Gamma(1 - z) \zeta(1 - z) $$ ($\Gamma(z)$ è la funzione Gamma di Eulero, anche questa visualizzabile con ImMap) dove compare il termine $\sin \left( \frac{\pi z}{2} \right)$. Gli zeri non banali sono invece l'argomento della famosa ipotesi di Riemann, uno dei più importanti problemi aperti della matematica.

L'ipotesi di Riemann afferma che gli zeri non banali hanno tutti parte reale pari ad $1 / 2$, sono quindi disposti nella cosiddetta retta critica $Re(z) = 1/2$. Si può dimostrare che essi si trovano tutti nella striscia critica $0 \lt Re(z) \lt 1$ e sono simmetrici sia rispetto alla retta critica che rispetto all'asse reale.

Hardy (ne approfitto per consigliare la lettura del suo Apologia di un matematico) ha dimostrato che ci sono infiniti zeri sulla retta critica e è stata verificata la veridicità dell'ipotesi per i primi $10^{13}$ zeri (nel 2014 da Xavier Gourdon, usando l'algoritmo Odlyzko-Schönhage), ma l'ipotesi resta ancora indimostrata.

La formula esplicita

La formula esplicita, che collega la funzione zeta di Riemann con la seconda funzione di Chebyshev, è costituita da 4 termini. Il primo ha segno positivo e vale $$ \frac{x^1}{1} = x $$ (il senso di esplicitare esponente e denominatore unitario, ininfluenti, è per coerenza con i termini successivi) e corrisponde al punto in cui la funzione zeta ha una singolarità (un polo semplice, quindi un punto in cui il modulo della funzione tende ad infinito). Questo termine determina la pendenza generale: la nostra scalinata avrà pendenza $1$ (la derivata di $x$), cioè 45 gradi.

I rimanenti termini sono sottratti al primo. Il secondo termine è una costante, la derivata logaritmica della funzione zeta in $0$ $$ \frac{\zeta'(0)}{\zeta(0)} = \ln \, 2 \pi $$ quindi il rapporto tra la derivata della funzione e il suo valore nell'origine del piano complesso. Questo termine non fa altro che traslare verso il basso la nostra scalinata, abbassandola di $\ln \, 2 \pi$, cioè circa $1.8$.

Il terzo termine corrisponde alla somma degli infiniti zeri banali $-2k$ nella forma $x^{-2k} / {-2k}$ $$ \sum_k \frac{x^{-2k}}{-2k} = \frac{1}{2} \ln \left( 1 - \frac{1}{x^2} \right) $$ con $k \in \mathbb{N^+}$. Questo termine tende a $0$ molto velocemente e influisce significativamente solo sui primi 2 o 3 gradini. In particolare, combaciando perfettamente con il quarto e ultimo termine, rende orizzontale il primo gradino (da ascissa $1$ a $2$) che corrisponde agli $0$ primi inferiori a $2$.

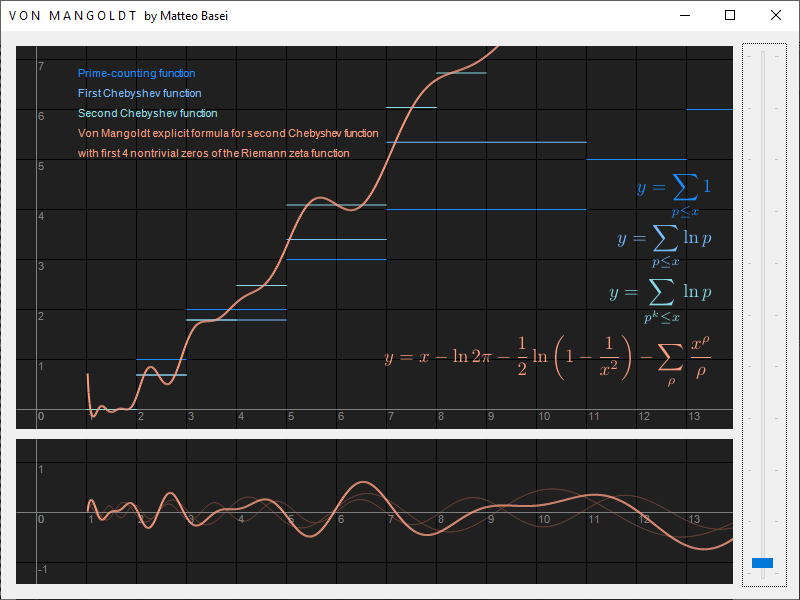
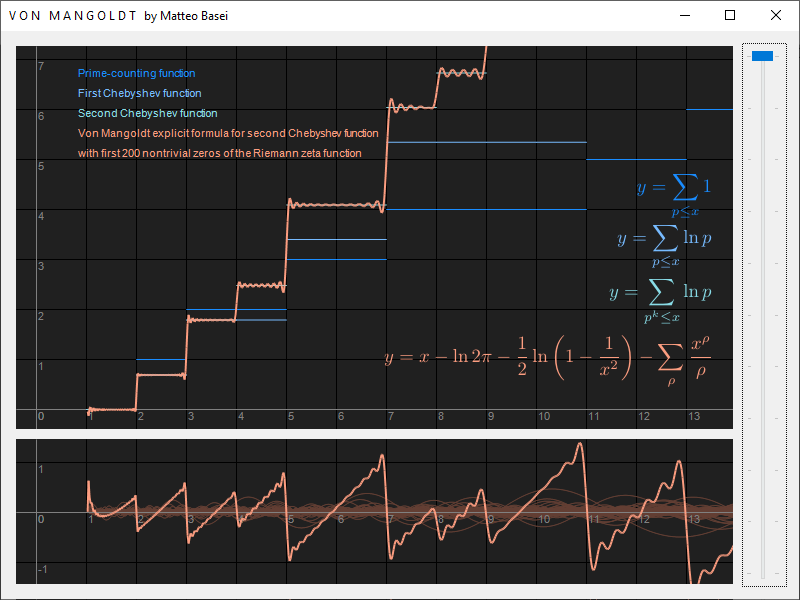
Il quarto termine, molto simile al precedente, corrisponde alla somma degli infiniti zeri non banali $\rho$ nella forma $x^\rho / \rho$. $$ \sum_\rho \frac{x^\rho}{\rho} $$ Questo termine è quello che effettivamente trasforma lo scivolo determinato dai 3 termini precedenti in una vera e propria scalinata. Nel programma, muovendo il cursore a destra, si può modificare il numero di zeri non banali usati in quest'ultima sommatoria, da un minimo di $0$ ad un massimo di $200$ (quindi da un minimo di $0$ ad un massimo di $100$ coppie).

Nel riquadro principale viene quindi disegnato il grafico della funzione $$ x - \ln \, 2 \pi - \frac{1}{2} \ln \left( 1 - \frac{1}{x^2} \right) - \sum_\rho \frac{x^\rho}{\rho} $$ Come si vede a differenza della funzione di enumerazione dei numeri primi, che come abbiamo già visto è asintotica a $x / \ln \left( x \right)$, la formula esplicita, e quindi la seconda funzione di Chebyshev, è asintotica a $x$ posto che gli zeri non banali abbiano tutti parte reale strettamente minore di $1$.

Le singole note

Passiamo ad analizzare un po' più in dettaglio il quarto termine in cui compaiono gli zeri non banali della funzione zeta. Sfruttando la simmetria degli zeri non banali rispetto all'asse reale li ordiniamo secondo il valore assoluto della parte immaginaria e in modo che $\rho_{2 k + 1} = \rho_{2 k}^*$ con $k \in \mathbb{N}$. Le singole "note" controllate dal cursore, una per ogni coppia di zeri non banali, sono quindi $$ \frac{x^{\rho_{2k}}}{\rho_{2k}} + \frac{x^{\rho_{2k}^*}}{\rho_{2k}^*} $$ che grazie alla presenza del complesso coniugato sono termini reali.

Inoltre secondo l'ipotesi di Riemann gli zeri non banali sono tutti nella forma $\rho_k = \frac{1}{2} + i \, \theta_k$. Quindi i termini $$ x^{\rho_k} = x^{\frac{1}{2} + i \, \theta_k} $$ essendo che $a^{b + c} = a^b a^c$ e $a^{1 / 2} = \sqrt{a}$, diventano $$ x^{\rho_k} = \sqrt{x} \, x^{i \, \theta_k} $$ e sono quindi sinusoidi ad ampiezza e lunghezza d'onda crescente (vedi Argand.exe, nella sezione riguardante l'identità di Eulero, per l'interpretazione geometrica di un'esponenziale con base reale ed esponente immaginario puro).

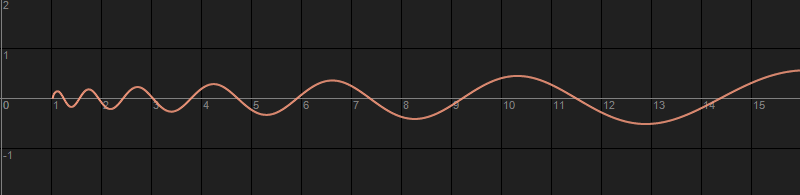
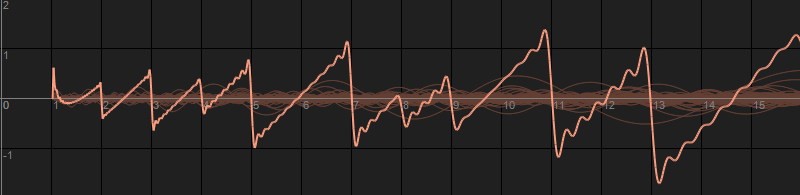
Nel riquadro in basso viene mostrato separatamente il grafico del quarto termine, incluse le singole "note", una per ogni coppia di termini della sommatoria. Si vede quindi come la sommatoria di questi termini generi una sorta di onda a dente di sega irregolare, che sottratta agli altri termini della formula porta ad approssimare sempre meglio i gradini della seconda funzione di Chebyshev. Se fosse possibile inserire nella sommatoria tutti gli infiniti zeri si otterrebbe una corrispondenza perfetta.

Possiamo quindi dire che questa sommatoria costituisce una sorta di scomposizione di Fourier (vedi Fourier.exe) della seconda funzione di Chebyshev, con la differenza che le sinusoidi hanno ampiezza crescente in funzione di $\sqrt{x}$ e lunghezza d'onda crescente in funzione di $x$.

In un certo senso questo straordinario legame risolve il problema della distribuzione dei numeri primi: la sequenza è perfettamente determinabile, è sufficiente conoscere l'esatta distribuzione di tutti gli zeri non banali della funzione zeta...

Significato geometrico dell'ipotesi di Riemann

Grazie al programma, in cui ho inserito un apposito cursore che permette di modificare la parte reale degli zeri non banali utilizzati nella somma, si può vedere empiricamente come questo valore determini l'inclinazione dei gradini. Solo con parte reale pari ad $1 / 2$ i gradini sono orizzontali e possono quindi corrispondere ai gradini della seconda funzione di Chebyshev, come dimostrato da von Mangoldt.

Le derivate dei primi due termini della formula sono banali ($1$ e $0$ rispettivamente), e anche la derivata del terzo termine si ottiene facilmente, ponendo infatti $t = 1 - 1 / x^2$, essendo $d \left( \ln t \right) / dt = 1 / t$ e $d \left( 1 - \frac{1}{x^2} \right) / dx = 2 / x^3$, si ha $$ \frac{1}{2} \frac{d \ln t}{dt}\frac{dt}{dx} = \frac{1}{2 \, t} \frac{dt}{dx} = \frac{1}{2 \left( 1 - \frac{1}{x^2} \right)} \frac{2}{x^3} = \frac{1}{x^3 - x} $$ Ovviamente il quarto termine, la sommatoria sugli zeri non banali, è quello problematico. La sua derivata deve essere pari a $1 - \frac{1}{x^3 - x}$ per $x > 1$ a meno di un'infinità numerabile di punti isolati (i "salti" dei gradini), in modo tale che la derivata della formula completa sia pari a $0$ (sempre a meno di un'infinità numerabile di punti isolati), il che corrisponde all'orizzontalità dei gradini. Dimostrare che ciò è possibile SOLO SE la parte reale degli zeri non banali è pari ad $1 / 2$ (che è ben diverso dal verificare empiricamente che ciò è vero utilizzando un centinaio di zeri), significherebbe dimostrare l'ipotesi di Riemann.