Mandelbrot.exe lungo l'orlo dell'infinito

"Le nuvole non sono sfere, le montagne non sono coni, le coste non sono cerchi e la corteccia non è liscia, né i fulmini viaggiano in linea retta."

L'insieme di Mandelbrot è l'insieme dei numeri complessi $c$ per i quali la successione $\left\{ z_n \right\}_{n \in \mathbb{N}}$ definita da $$ \begin{alignedat}{2} z_0 &= 0 \\ z_{n + 1} &= z_n^2 + c \end{alignedat} $$ è limitata (cioè per i quali esiste un $M$ tale che $\left| z_n \right| \le M \, \forall n \in \mathbb{N}$). Se i numeri complessi non ti sono familiari potresti dare un'occhiata al mio programma Argand.exe prima di continuare.

Questa definizione è dovuta a Adrien Douady (facente parte dell'ultima generazione di membri del famoso gruppo Bourbaki), che nominò l'insieme in onore di Benoit Mandelbrot, pioniere nello studio della geometria frattale. Il termine frattale è stato coniato da Mandelbrot stesso, mutuandolo dal latino "fractus", spezzare, frantumare.

In base alla definizione la successione inizia quindi con i seguenti termini $$ \begin{alignedat}{2} z_0 &= 0 \\ z_1 &= c \\ z_2 &= c^2 + c \\ z_3 &= (c^2 + c)^2 + c \\ z_4 &= ((c^2 + c)^2 + c)^2 + c \\ ... \end{alignedat} $$

Partendo da un determinato numero $c$, e quindi da un determinato punto nel piano complesso, possono succedere due cose: o la traiettoria individuata dai vari $z_n$ si ritorce su se stessa, restando sempre in una zona limitata del piano (successione limitata) oppure la traiettoria si "srotola" verso l'infinito (successione divergente). Nel primo caso il punto $c$ appartiene all'insieme di Mandelbrot, nel secondo caso no.

A dispetto di una definizione tanto semplice il bordo dell'insieme di Mandelbrot è un frattale estremamente vario e complesso. È inoltre notevole il fatto che, nonostante le apparenze, tale insieme è connesso, cioè è costituito da un "unico pezzo", come dimostrato dallo stesso Douady.

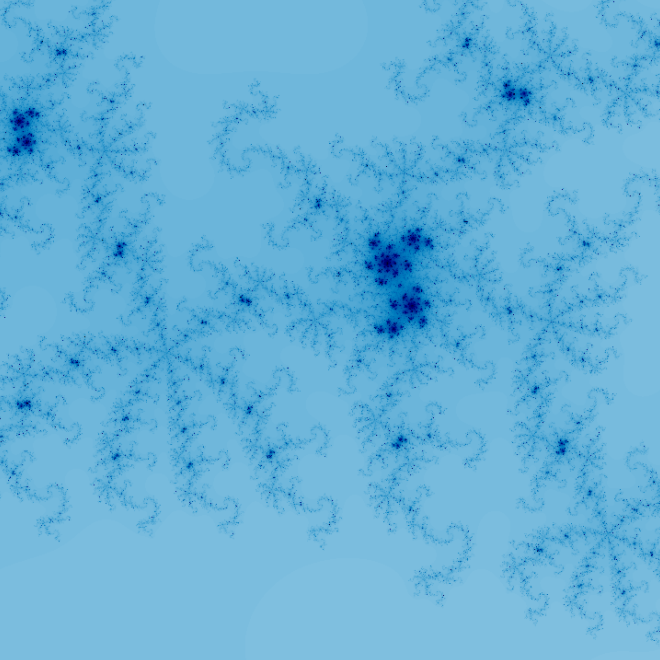
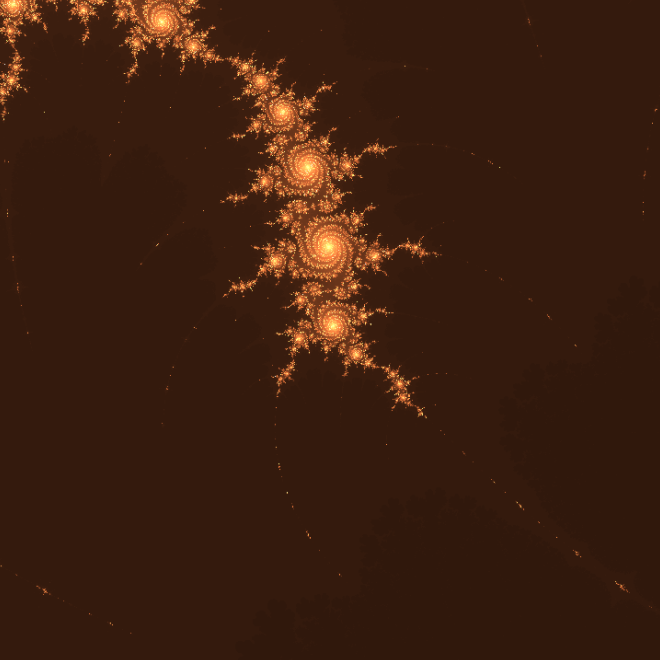
A rigore, rappresentando l'insieme di Mandelbrot, ci sono solo due tipi di punti da visualizzare: quelli che fanno parte dell'insieme e quelli che non ne fanno parte. È poi uso comune colorare i punti che non fanno parte dell'insieme con intensità collegate a quanto velocemente la successione diverge. In particolare si utilizza il modulo dell'ultimo $z_n$ quando è diventato maggiore di $2$ (si può dimostrare che quando il modulo diventa maggiore di $2$ la successione divergerà) oppure il numero di iterazioni eseguite prima che ciò sia avvenuto.

Spesso si vedono usati colori di vario tipo in vari modi, sempre legati al comportamento delle successioni divergenti. In questa implementazione, a differenza di molte altre viste altrove, ho volutamente ridotto al minimo l'uso dei colori, per far "venir fuori" il più possibile la complessità dell'insieme così com'è, senza artifici o aggiunte.

Puoi trovare altro riguardo l'insieme di Mandelbrot e altri frattali ad esso collegati in questa pagina.

Riguardo i frattali che si possono ottenere considerando funzioni differenti da $f(z) = z^2 + c$, potrebbe invece interessarti quest'altra pagina.

Infine per una definizione generale di frattale, indipendente dal piano complesso, puoi dare un'occhiata al paragrafo "Dimensione algebrica, topologica e frattale" nella mia pagina sugli algoritmi ricorsivi R-Paint.