Argand.exe la semplice geometria complessa

"Se questo argomento è stato finora considerato dal punto di vista sbagliato e avvolto da una misteriosa oscurità, è da attribuire in gran parte ad una terminologia inadatta. Se ad esempio a $+1$, $-1$ e $\sqrt{-1}$ fossero stati dati i nomi di unità diretta, inversa e laterale, invece di positiva, negativa e immaginaria (o addirittura impossibile), tale oscurità sarebbe stata fuori questione."

Jean-Robert Argand fu un matematico svizzero non professionista che nel 1806, mentre lavorava in una libreria di Parigi, propose l'interpretazione geometrica dei numeri complessi (anche se, a onor del vero, il primo a proporla fu il matematico norvegese Caspar Wessel nel 1797, in una pubblicazione in lingua danese che al tempo passò pressoché inosservata). In suo onore ancora oggi il piano complesso è a volte chiamato piano di Argand-Gauss, e in suo onore ho chiamato Argand.exe questa semplice applicazione, che aiuta a visualizzare i numeri complessi e le operazioni tra essi.

Un numero complesso $z \in \mathbb{C}$ è un numero nella forma $$ z = a + i \, b $$ dove $a , b \in \mathbb{R}$ e $i = \sqrt{-1}$ è l'unità immaginaria. $\mathbb{R}$ è l'insieme dei numeri reali, che possono essere messi in corrispondenza con i punti della retta.

La rappresentazione dei numeri complessi nel piano complesso nasce invece dalla corrispondenza tra un numero complesso $x + i \, y \in \mathbb{C}$ e un vettore $\left( x , y \right) \in \mathbb{R}^2$ del piano cartesiano. $\mathbb{R}^2$, facendo il verso all'elevamento a potenza tra numeri, indica $\mathbb{R} \times \mathbb{R}$, il prodotto cartesiano dell'insieme $\mathbb{R}$ per se stesso. In generale tra due insiemi $A$ e $B$ il prodotto cartesiano è definito come l'insieme costituito da tutte le possibili coppie $\left( a , b \right)$ con $a \in A$ e $b \in B$. Nella rappresentazione grafica del piano la convenzione è che l'asse reale sia orizzontale con il verso positivo verso destra, mentre l'asse immaginario, dove giace $i$, sia verticale con verso positivo verso l'alto.

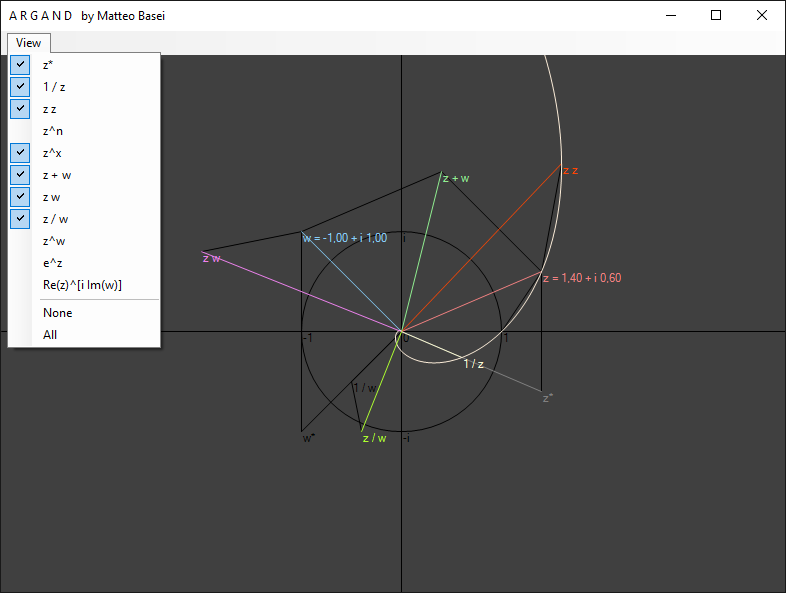
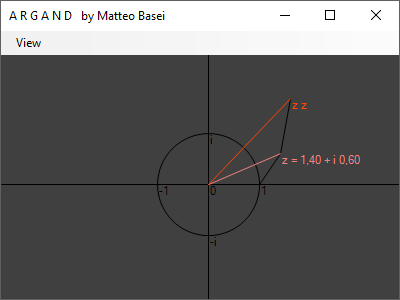
In questo programma sono visualizzati due numeri complessi, $z$ e $w$, rispettivamente in rosso e azzurro. Con il mouse, tenendo premuto il pulsante sinistro e destro rispettivamente, è possibile posizionare a piacere $z$ e $w$ nel piano complesso. Con un menù a tendina è inoltre possibile attivare e disattivare la visualizzazione di vari numeri complessi da essi derivati.

Complesso coniugato e reciproco

Il primo di questi è il complesso coniugato di $z$ $$ z^* = a - i \, b $$ la cui interpretazione geometrica corrisponde semplicemente ad una riflessione avente come asse di simmetria l'asse reale.

Notiamo che sfruttando il fatto che $i^2 = -1$ si ha $$ \begin{alignedat}{2} z \, z^* &= \left( a + i \, b \right) \left( a - i \, b \right) = \\ &= a^2 - i \, a \, b + i \, b \, a - i^2 b^2 = \\ &= a^2 - i^2 b^2 = \\ &= a^2 + b^2 \end{alignedat} $$ e quindi essendo $$ \left| z \right| = \sqrt{a^2 + b^2} $$ il modulo di $z$, cioè la lunghezza del corrispondente vettore in $\mathbb{R}^2$ calcolata con il teorema di Pitagora, otteniamo $$ z \, z^* = \left| z \right|^2 $$ Abbiamo quindi dimostrato che il prodotto tra un numero complesso e il suo complesso coniugato è un numero reale uguale al quadrato del modulo, pur non avendo ancora definito in generale la moltiplicazione tra numeri complessi.

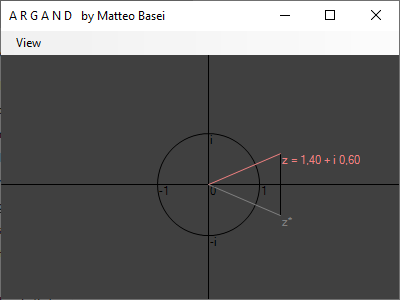
Allo stesso modo questo ci permette, senza aver una nozione di divisione tra numeri complessi, di calcolare facilmente il reciproco di $z$. Moltiplicando infatti numeratore e denominatore di $1 / z$ per $z^*$ otteniamo $$ \frac{1}{z} = \frac{z^*}{z \, z^*} = \frac{z^*}{\left| z \right|^2} $$ quindi il reciproco di $z$ è un numero complesso avente direzione di $z^*$ e modulo pari al reciproco del modulo di $z$.

La regola del parallelogramma

Pur avendo già visto casi particolari di prodotto e divisione con $z \, z^*$ e $1 / z$ grazie alle proprietà della coniugazione complessa, non abbiamo ancora verificato il comportamento nemmeno della somma di numeri complessi. La cosa è in realtà molto semplice, algebricamente abbiamo semplicemente $$ \begin{alignedat}{2} z + w &= \left( a + i \, b \right) + \left( c + i \, d \right) = \\ &= \left( a + c \right) + i \left( b + d \right) \end{alignedat} $$ dove non si sfrutta in alcun modo le proprietà dei numeri immaginari, ma semplicemente la proprietà distributiva della moltiplicazione rispetto all'addizione per raccogliere $i$ e ritrovarci con un'espressione nella stessa forma di $a + i \, b$. L'interpretazione geometrica di ciò è l'altrettanto semplice regola del parallelogramma.

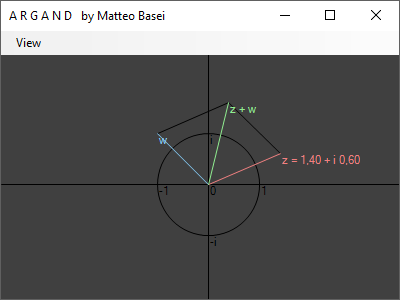
La regola del parallelogramma emerge per il semplice fatto che la somma di numeri complessi in $\mathbb{C}$ corrisponde esattamente alla somma di vettori bidimensionali nel piano $\mathbb{R}^2$.

La regola dei triangoli simili

Per la moltiplicazione $z \, w$, grazie al fatto che $i^2 = -1$, si ottiene $$ \begin{alignedat}{2} z \, w &= \left( a + i \, b \right) \left( c + i \, d \right) = \\ &= a \, c + i \left( a \, d + b \, c \right) + i^2 \, b \, d = \\ &= \left( a \, c - b \, d \right) + i \left( a \, d + b \, c \right) \end{alignedat} $$ che è ancora nella forma di un numero complesso $a + i \, b$. Quindi anche il prodotto tra due numeri complessi, così come la somma, è ancora un numero complesso.

Si verifica facilmente che il prodotto tra due numeri complessi corrisponde alla moltiplicazione dei moduli e alla somma delle fasi. La fase di un numero complesso $z$, indicata con $\arg(z)$, è l'angolo, misurato in radianti e in senso antiorario, sotteso tra il corrispondente vettore in $\mathbb{R}^2$ e il semiasse positivo dell'asse reale.

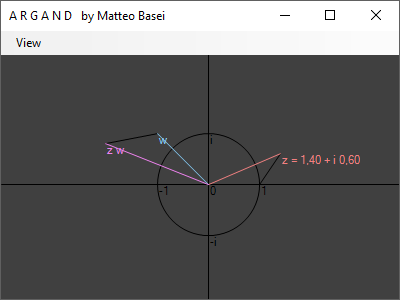
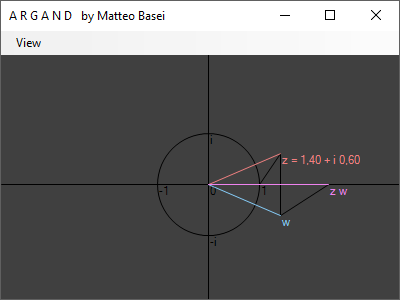
Tale trasformazione può essere interpretata attraverso la cosiddetta regola dei triangoli simili: il triangolo avente vertici $0$, $1$ e $z$ avrà la stessa forma del triangolo formato dai vertici $0$, $w$ e $z \, w$.

In particolare quindi la moltiplicazione per un numero che giace nel cerchio unitario corrisponde ad una rotazione pura e la moltiplicazione per $i$ corrisponde quindi ad una rotazione di $90^\circ$.

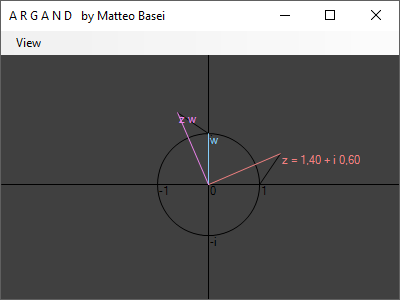
Vediamo come la moltiplicazione complessa in generale sia in accordo con il caso particolare visto all'inizio della moltiplicazione $z \, z^*$ di un numero complesso per il proprio complesso coniugato. Il risultato avrà come modulo il prodotto dei moduli, quindi $\left| z \right|^2$, e come fase la somma delle fasi, che in questo caso si annullano e ci danno un numero reale.

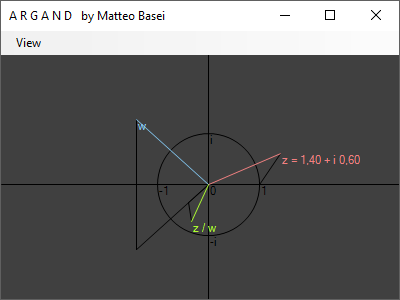
Infine vediamo che $$ \frac{z}{w} = z \frac{1}{w} = z \frac{w^*}{\left| w \right|^2} $$ quindi per la divisione si applica ancora la regola dei triangoli simili, ma questa volta tra $z$ e il reciproco di $w$, che sarà nella direzione del complesso coniugato $w^*$.

L'elevamento a potenza

L'elevamento a potenza è l'operazione in cui i numeri complessi danno il meglio di se (cosa tra l'altro collegata direttamente al famoso insieme di Mandelbrot).

Ovviamente $z^2$ non è altro che $z \, z$, quindi ricadiamo ancora nella regola dei triangoli simili. I due triangoli in questo caso sono "appoggiati" l'uno sull'altro, e il risultato fa sorgere spontanea una possibile evoluzione: cosa succede iterando questa operazione?

Questo porta a considerare la sequenza di valori che si ottengono elevando $z$ per una successione crescente di numeri, molto interessante dal punto di vista geometrico. Iniziamo consideranto gli interi non negativi, quindi $z^n$ con $n \in \mathbb{N}$. La sequenza parte sempre da $1$, infatti $z^0 = 1$ per ogni scelta di $z$.

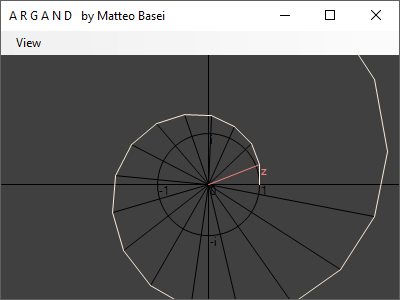
Spostando $z$ nel piano complesso si ottiene un moltitudine di figure differenti. Prima di tutto se $z$ giace all'interno del cerchio unitario la spezzata sarà ritorta su se stessa, mentre se $z$ resta esterno al cerchio unitario avremo una figura che si "srotolerà" all'infinito. Inoltre scegliendo punti prossimi ad $1$ otterremo delle forme a spirale via via più "continue" mano a mano che ci avviciamo ad $1$. Avvicinandosi a $-1$ otterremo invece figure via via più discontinue ed elaborate.

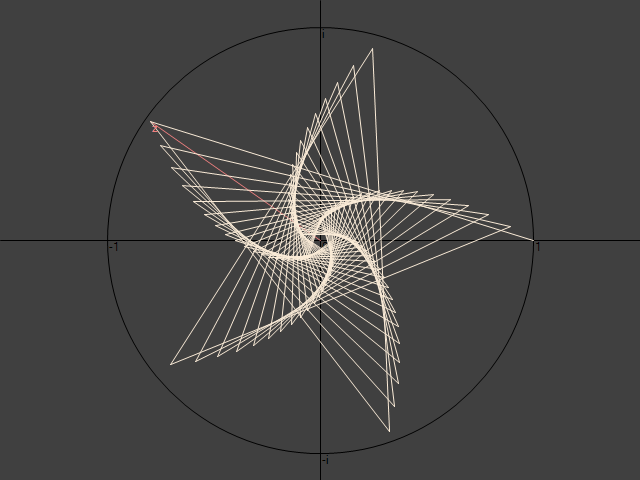
La varietà di forme è tale che meriterebbero una pagina a se stante per elencarne almeno le più importanti. Qui mi limito ad un paio di esempi tra i più interessanti esteticamente.

Passando ad esponente reale, quindi $z^x$ con $x \in \mathbb{R}$, otteniamo semplicemente l'interpolazione delle figure ottenibili con esponente intero. Indipendetemente dalla base si ottiene una spirale, perdendo quindi la varietà delle forme ottenibili con esponente intero, dovute alla discontinuità di quest'ultimo.

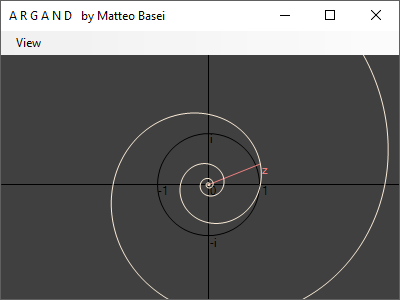
Prendendo valori sia positivi che negativi si ottiene sempre una spirale completa che da un lato diverge verso l'infinito e dall'altro converge verso $0$. Con base interna al cerchio unitario la parte interna della spirale sarà costituita dai termini con esponente positivi, quella esterna dai termini con esponente negativi. Con base esterna al cerchio unitario si avrà l'opposto.

Abilitando la visualizzazione sia di $z^x$ sia di $1 / z$ si può vedere come quest'ultimo tocchi sempre la spirale in un punto, che non è altro che la rappresentazione geometrica del fatto che $z^{-1} = 1 / z$.

L'identità di Eulero

Quando la base $z$ è un numero reale positivo e l'esponente $w$ è un numero immaginario puro $z^w$ giace nella circonferenza unitaria. Poniamo quindi $z = x$ e $w = i \, \theta$ con $0 < x \in \mathbb{R}$ e $\theta \in \mathbb{R}$ e consideriamo il comportamento di $$ x^{i \, \theta} $$ Incrementando $\theta$ il risultato di $x^{i \, \theta}$ ruota in senso antiorario, partendo da $x^{i \, 0} = 1$ fino a tornare a $1$ dopo aver percorso l'intero cerchio unitario. A seconda della scelta della base $x$ la rotazione sarà, a parità di variazione di $\theta$, più o meno ampia.

Questo tra l'altro fa si $x^{i \, \theta}$ ruoti intorno all'origine anche mantenendo fisso $\theta$ e variando $x$ (ma, in questo caso, come abbiamo già sottolineato, solo per valori positivi di $x$), cosa importante per il collegamento tra la distribuzione dei numeri primi e gli zeri della funzione zeta di Riemann (vedi VonMangoldt.exe).

Mantenendo fisso $x$ e variando $\theta$ invece $x^{i \, \theta}$ compie un intero giro intorno all'origine quando $\theta$ raggiunge un certo valore che è determinato dalla scelta di $x$. La scelta più naturale per questo tale valore di $\theta$ sarà il doppio di pi greco, essendo $2 \pi$ la lunghezza della circonferenza di raggio unitario. Risulta che la scelta di $x$ per ottenere un giro completo quando $\theta = 2 \pi$ è $$ e = 2,718281... $$ cioè la base dei logaritmi naturali.

Il motivo è che $$ \frac{d}{d \theta} e^{i \, \theta} = i \, e^{i \, \theta} $$ quindi $e^{i \, \theta}$ al variare di $\theta$ ruota con velocità $1$ (la moltiplicazione per $i$ corrisponde ad una rotazione di 90 gradi).

In altre parole scegliendo una base inferiore ad $e$ la velocità di rotazione al variare di $\theta$ sarà inferiore a $1$ e il valore di $\theta$ dovrà arrivare oltre $2 \pi$ prima che $x^{i \, \theta}$ completi il suo giro. Di contro scegliendo una base superiore ad $e$ il giro sarà completato con un esponente inferiore. Scegliendo $x = e$ il valore da raggiungere sarà esattamente $\theta = 2 \pi$.

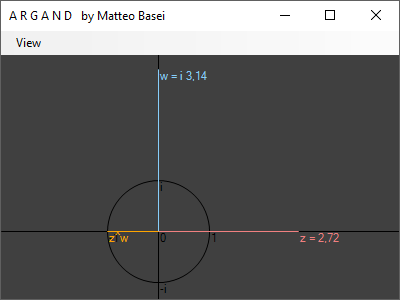
Quindi quando $\theta = \pi$ avremo percorso mezzo giro intorno all'origine e saremo quindi arrivati a $-1$. Questa è l'interpretazione geometrica della meravigliosa identità di Eulero $$ e^{i \, \pi} + 1 = 0 $$ una delle più famose e belle formule di tutta la matematica. Essa unisce in un unica formula $0$, $1$, $i$, $\pi$ ed $e$, combinandoli con somma, moltiplicazione ed elevamento a potenza.

E tanto altro...

I numeri complessi sono entrati nella matematica ben prima della scoperta da parte di Wessel, Argand e Gauss della loro meravigliosa interpretazione geometrica. Già nel XVI secolo venivano utilizzati, seppur considerati come meri artifici per il calcolo, per la risoluzione delle equazioni di terzo e quarto grado da matematici come Scipione del Ferro, Tartaglia e Cardano.

Dopo un'iniziale reticenza si sono poi diffusi, ed ora i numeri complessi pervadono tutte le aree della scienza. Per fare alcuni esempi:

• in algebra, come abbiamo in parte visto, preservano tutte le proprietà dei numeri reali (con le operazioni di somma e prodotto formano un campo, un anello commutativo senza divisori dello zero), costituendone inoltre la cosiddetta chiusura algebrica, il che rende $\mathbb{C}$ il campo per antonomasia ancor più di quanto lo sia $\mathbb{R}$;
• in analisi le funzioni complesse a variabile complessa giocano un ruolo fondamentale, una funzione derivabile in senso complesso è automaticamente liscia (derivabile infinite volte) e analitica (esprimibile come serie di potenze). La semplice funzione $1 / x$, discontinua e "spezzata" brutalmente in due nel campo reale, assume la sua più naturale forma nel campo complesso (vedi ImMap);
• in analisi armonica con la trasformata di Fourier (vedi Fourier.exe e F-Paint);
• in teoria dei numeri, con il già menzionato legame tra i numeri primi e la funzione Zeta di Riemann (vedi VonMangoldt.exe);
• in geometria frattale, vedi il già citato insieme di Mandelbrot (vedi anche Julia);
• in molti ambiti della fisica e dell'ingegneria, per la loro caratteristica di essere la naturale rappresentazione di fenomeni oscillanti (l'ombra di una rotazione è un'oscillazione, vedi Lissajous), ad esempio in elettronica analogica;
• in fisica teorica, con il ruolo centrale che hanno in meccanica quantistica (vedi QED.exe).